
如图,底面为直角梯形的四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,E为A1B1的中点,且△ABE为等腰直角三角形,AB∥CD,AB⊥BC,AB=2CD=2BC.
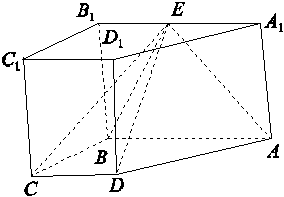
(1)求证:AB⊥DE;
(2)求直线EC与平面ABE所成角的正弦值;
(3)线段EA上是否存在点F,使EC∥平面FBD?若存在,求出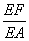 ;若不存在,请说明理由.
;若不存在,请说明理由.
解:(1)证明:取AB中点O,连接EO,DO.
因为EB=EA,所以EO⊥AB.
因为四边形ABCD为直角梯形,
AB=2CD=2BC,AB⊥BC,
所以四边形OBCD为正方形,
所以AB⊥OD.
又EO,OD为平面EOD内的两条相交直线,
所以AB⊥平面EOD.
因为ED⊂平面EOD,
所以AB⊥ED.
(2)因为AA1⊥平面ABCD,且EO∥AA1,
所以EO⊥平面ABCD,所以EO⊥OD.
由OD,OA,OE两两垂直,建立如图所示的空间直角坐标系O-xyz.
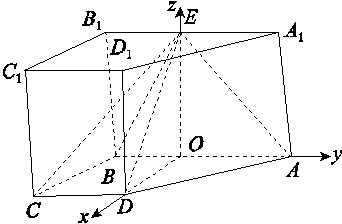
因为△EAB为等腰直角三角形,
所以OA=OB=OD=OE,设OB=1,
则O(0,0,0),A(0,1,0),B(0,-1,0),C(1,-1,0),D(1,0,0),E(0,0,1).
所以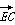 =(1,-1,-1),平面ABE的一个法向量为
=(1,-1,-1),平面ABE的一个法向量为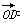 =(1,0,0).
=(1,0,0).
设直线EC与平面ABE所成的角为θ,
所以sin θ=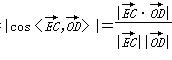 =
=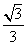 ,
,
即直线EC与平面ABE所成角的正弦值为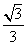 .
.
(3)存在点F,且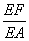 =
=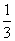 时,有EC∥平面FBD.证明如下:
时,有EC∥平面FBD.证明如下:
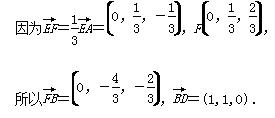 设平面FBD的法向量为ν=(a,b,c),
设平面FBD的法向量为ν=(a,b,c),
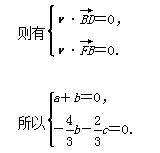 取a=1,
取a=1,
得ν=(1,-1,2).
因为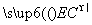 ·ν=(1,-1,-1)·(1,-1,2)=0,
·ν=(1,-1,-1)·(1,-1,2)=0,
即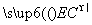 ⊥ν;
⊥ν;
又因为EC⊄平面FBD,
所以EC∥平面FBD.
因此当点F满足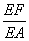 =
=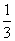 时,有EC∥平面FBD.
时,有EC∥平面FBD.


科目:高中数学 来源: 题型:
两圆(x-2)2+(y+3)2=13和(x-3)2+y2=9交于A,B两点,则AB的垂直平分线的方程是( )
A.x+y+3=0 B.2x-y-5=0 C.3x-y-9=0 D.4x-3y+7=0
查看答案和解析>>
科目:高中数学 来源: 题型:
某学校组织演讲比赛,准备从甲、乙等8名学生中选派4名学生参加,要求甲、乙两名同学至少有一人参加,且若甲、乙同时参加时,他们的演讲顺序不能相邻,那么不同的演讲顺序的种类为( )
A.1 860 B.1 320 C.1 140 D.1 020
查看答案和解析>>
科目:高中数学 来源: 题型:
已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列命题:
①若α⊥β,m∥α,则m⊥β;
②若m⊥α,n⊥β,且m⊥n,则α⊥β;
③若m⊥β,m∥α,则α⊥β;
④若m∥α,n∥β,且m∥n,则α∥β.
其中正确命题的序号是( )
A.①④ B.②③
C.②④ D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f(n)=logn+1(n+2)(n∈N*),定义使f(1)·f(2)·f(3)·…·f(k)为整数的数k(k∈N*)叫做企盼数,则在区间[1,2 013]内这样的企盼数共有________个.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知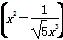 5的展开式中的常数项为T,f(x)是以T为周期的偶函数,且当x∈[0,1]时,f(x)=x,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是________.
5的展开式中的常数项为T,f(x)是以T为周期的偶函数,且当x∈[0,1]时,f(x)=x,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com