练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知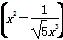5的展开式中的常数项为T，f(x)是以T为周期的偶函数，且当x∈[0,1]时，f(x)＝x，若在区间[－1,3]内，函数g(x)＝f(x)－kx－k有4个零点，则实数k的取值范围是________．


    [解析]　Tk＋1＝C(x2)5－k·kCx10－5k，

    常数项为10－5k＝0，即k＝2，所以T3＝2C＝2.函数f(x)是周期为2的偶函数，其图象如图所示．

    函数g(x)＝f(x)－kx－k有4个零点，说明函数y＝f(x)与直线y＝kx＋k有四个交点，直线y＝kx＋k是过定点(－1,0)的直线．如图可知当直线y＝kx＋k为图中直线l位置时符合题意，当直线y＝kx＋k过点A(3,1)时，k＝，故满足条件k的范围为.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知实数x，y满足：的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，底面为直角梯形的四棱柱ABCD－A1B1C1D1中，侧棱AA1⊥底面ABCD，E为A1B1的中点，且△ABE为等腰直角三角形，AB∥CD，AB⊥BC，AB＝2CD＝2BC.

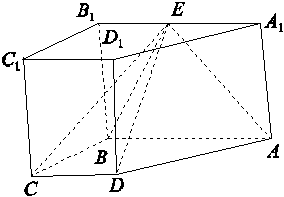
    (1)求证：AB⊥DE；

    (2)求直线EC与平面ABE所成角的正弦值；

    (3)线段EA上是否存在点F，使EC∥平面FBD？若存在，求出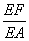；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝asin2x＋bx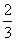＋4(a，b∈R)，若f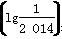＝2 013，则f(lg 2 014)＝(　　)

    A．2 018  B．－2 009  C．2 013  D．－2 013

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝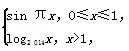

    若a，b，c互不相等，且f(a)＝f(b)＝f(c)，则a＋b＋c的取值范围是(　　)

    A．(1,2 014)                            B．(1,2 015) 

    C．(2,2 015)                            D．[2,2 015]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)是定义域为R的奇函数，且x≤0时，f(x)＝2x－x＋a，则函数f(x)的零点个数是(　　)

    A．1  B．2  C．3  D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知t>－1，当x∈[－t，t＋2]时，函数y＝(x－4)|x|的最小值为－4，则t的取值范围________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知g(x)＝－x2－4，f(x)为二次函数，满足f(x)＋g(x)＋f(－x)＋g(－x)＝0，且f(x)在[－1,2]上的最大值为7，则f(x)＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)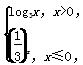＝那么不等式f(x)≥1的解集为(　　)

    A．{x|－3≤x≤0}                        B．{x|x≤－3或x≥0}

    C．{x|0≤x≤3}                          D．{x|x≤0或x≥3}

    查看答案和解析>>

    同步练习册答案