练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f(x)是定义域为R的奇函数，且x≤0时，f(x)＝2x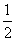－x＋a，则函数f(x)的零点个数是(　　)

    A．1  B．2  C．3  D．4


    C

    [解析]　由题意知，f(0)＝0，∴a＝－1，∴f(x)＝2x－x－1.在同一坐标系中分别作出y＝2x和y＝x＋1的图象知，当x<0时，有一解，又f(x)为奇函数．∴x>0时，有一解，又f(0)＝0，∴f(x)的零点有3个．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设不等式组表示区域为D，且圆x2＋y2＝4在D内的弧长为，则实数a的值等于________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝

    是(－∞，＋∞)上的减函数，那么实数a的取值范围是(　　)

    A．(0,1)     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，已知正方体ABCD－A1B1C1D1的棱长是1，点E是对角线AC1上一动点，记AE＝x(0<x<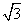)，过点E平行于平面A1BD的截面将正方体分成两部分，其中点A所在的部分的体积为V(x)，则函数y＝V(x)的图象大致为(　　)

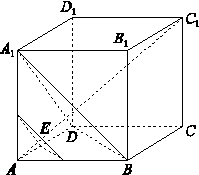
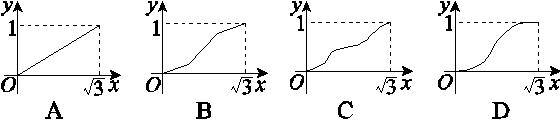
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知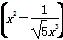5的展开式中的常数项为T，f(x)是以T为周期的偶函数，且当x∈[0,1]时，f(x)＝x，若在区间[－1,3]内，函数g(x)＝f(x)－kx－k有4个零点，则实数k的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：

    (1)对任意a∈R，a*0＝a；

    (2)对任意a，b∈R，a*b＝ab＋(a*0)＋(b*0)．

    关于函数f(x)＝(ex)*的性质，有如下说法：①函数f(x)的最小值为3；②函数f(x)为偶函数；③函数f(x)的单调递增区间为(－∞，0]．

    其中所有正确说法的个数为(　　)

    A．0                                    B．1 

    C．2                                    D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝(x－a)(x－b)(a>b)的图象如图所示，则函数g(x)＝ax＋b的图象是(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a＝2，b＝log2，c＝log，则(　　)

    A．a>b>c                                B．a>c>b 

    C．c>b>a                                D．c>a>b

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)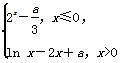＝有三个不同的零点，则实数a的取值范围是(　　)

    A．(0,3]                                B．(1＋ln 2,3]

    C．(1－ln 2,3]                          D．[－3,3]

    查看答案和解析>>

    同步练习册答案