
在实数集R中定义一种运算“*”,对任意a,b∈R,a*b为唯一确定的实数,且具有性质:
(1)对任意a∈R,a*0=a;
(2)对任意a,b∈R,a*b=ab+(a*0)+(b*0).
关于函数f(x)=(ex)* 的性质,有如下说法:①函数f(x)的最小值为3;②函数f(x)为偶函数;③函数f(x)的单调递增区间为(-∞,0].
的性质,有如下说法:①函数f(x)的最小值为3;②函数f(x)为偶函数;③函数f(x)的单调递增区间为(-∞,0].
其中所有正确说法的个数为( )
A.0 B.1
C.2 D.3
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
若x4(x+3)8=a0+a1(x+2)+a2(x+2)2+…+a12(x+2)12,则log2(a1+a3+a5+…+a11)=( )
A.27 B.28 C.7 D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
定义在R上的函数f(x)=ax3+bx2+cx(a≠0)的单调增区间为(-1,1),若方程3a(f(x))2+2bf(x)+c=0恰有6个不同的实根,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上是单调递增函数.如果实数t满足f(ln t)+f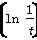 ≤2f(1),那么t的取值范围是________.
≤2f(1),那么t的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线C:x=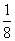 y2的焦点为F(m,0),点M的坐标为(-m,m),过C的焦点且斜率为k的直线与C交于A,B两点.若
y2的焦点为F(m,0),点M的坐标为(-m,m),过C的焦点且斜率为k的直线与C交于A,B两点.若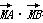 =0,则k=( )
=0,则k=( )
A.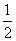 B.
B.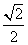 C.
C.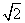 D.2
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( )
A.(2,+∞) B.(-∞,-2)
C.(1,+∞) D.(-∞,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com