定义在R上的函数f(x)＝ax3＋bx2＋cx(a≠0)的单调增区间为(－1,1)，若方程3a(f(x))2＋2bf(x)＋c＝0恰有6个不同的实根，则实数a的取值范围是________．
名校课堂系列答案科目：高中数学 来源： 题型：
等边三角形ABC的边长为3，点D，E分别是边AB，AC上的点，且满足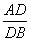
＝
＝
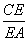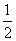(如图①)．将△ADE沿DE折起到△A1DE的位置，使二面角A1－DE－B为直二面角，连接A1B，A1C(如图②)．
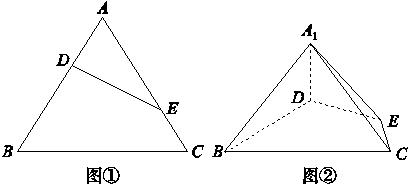
(1)求证：A1D⊥平面BCED；
(2)在线段BC上是否存在点P，使直线PA1与平面A1BD所成的角为60°？若存在，求出PB的长，若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知f(x)为定义在R上的偶函数，当x≥0时，有f(x＋1)＝－f(x)，且当x∈[0,1)时，f(x)＝log2(x＋1)，给出下列命题：
①f(2 013)＋f(－2 014)的值为0；
②函数f(x)在定义域上为周期是2的周期函数；
③直线y＝x与函数f(x)的图象有1个交点；
④函数f(x)的值域为(－1,1)．
其中正确命题的序号有________．
查看答案和解析>>
科目：高中数学 来源： 题型：
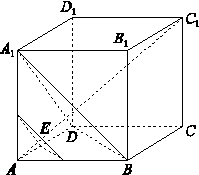
如图，已知正方体ABCD－A1B1C1D1的棱长是1，点E是对角线AC1上一动点，记AE＝x(0<x<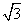
)，过点E平行于平面A1BD的截面将正方体分成两部分，其中点A所在的部分的体积为V(x)，则函数y＝V(x)的图象大致为( )
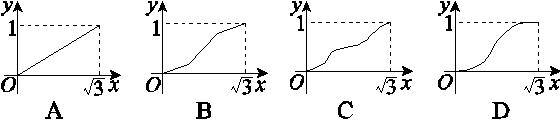
查看答案和解析>>
科目：高中数学 来源： 题型：
若函数f(x)＝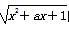
的定义域为实数集R，则实数a的取值范围为( )
A．(－2,2)
B．(－∞，－2)∪(2，＋∞)
C．(－∞，－2]∪[2，＋∞)
D．[－2,2]
查看答案和解析>>
科目：高中数学 来源： 题型：
在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：
(1)对任意a∈R，a*0＝a；
(2)对任意a，b∈R，a*b＝ab＋(a*0)＋(b*0)．
关于函数f(x)＝(ex)*
的性质，有如下说法：①函数f(x)的最小值为3；②函数f(x)为偶函数；③函数f(x)的单调递增区间为(－∞，0]．
其中所有正确说法的个数为( )
A．0 B．1
C．2 D．3
查看答案和解析>>
科目：高中数学 来源： 题型：
设f(x)是定义在R上的偶函数，且当x≥0时，f(x)＝2x.若对任意的x∈[a，a＋2]，不等式f(x＋a)≥f2(x)恒成立，则实数a的取值范围是________．
查看答案和解析>>
科目：高中数学 来源： 题型：
前不久，省社科院发布了2013年度“城市居民幸福排行榜”，某市成为本年度城市最“幸福城”．随后，某校学生会组织部分同学，用“10分制”随机调查“阳光”社区人们的幸福度．现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎，小数点后的一位数字为叶)：
(1)指出这组数据的众数和中位数；
(2)若幸福度不低于9.5分，则称该人的幸福度为“极幸福”．求从这16人中随机选取3人，至多有1人是“极幸福”的概率；
(3)以这16人的样本数据来估计整个社区的总体数据，若从该社区(人数很多)任选3人，记ξ表示抽到“极幸福”的人数，求ξ的分布列及数学期望．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
[解析] ∵函数f(x)＝ax3＋bx2＋cx(a≠0)的单调增区间为(－1,1)，∴－1和1是f′(x)＝0的根．
∴b＝0，c＝－3a.
∴a<－
.
则
的最大值是________．