练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若函数f(x)是定义在R上的偶函数，且在区间[0，＋∞)上是单调递增函数．如果实数t满足f(ln t)＋f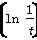≤2f(1)，那么t的取值范围是________．


    [解析]　由于函数f(x)是定义在R上的偶函数，所以f(ln t)＝f，由f(ln t)＋f≤2f(1)，得f(ln t)≤f(1)．又函数f(x)在区间[0，＋∞)上是单调递增函数，所以|ln t|≤1，－1≤ln t≤1，故≤t≤e.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    从甲、乙等5名志愿者中选出4名，分别从事A，B，C，D四项不同的工作，每人承担一项．若甲、乙二人均不能从事A工作，则不同的工作分配方案共有(　　)

    A．60种  B．72种  C．84种  D．96种

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)为定义在R上的偶函数，当x≥0时，有f(x＋1)＝－f(x)，且当x∈[0,1)时，f(x)＝log2(x＋1)，给出下列命题：

    ①f(2 013)＋f(－2 014)的值为0；

    ②函数f(x)在定义域上为周期是2的周期函数；

    ③直线y＝x与函数f(x)的图象有1个交点；

    ④函数f(x)的值域为(－1,1)．

    其中正确命题的序号有________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)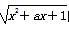＝的定义域为实数集R，则实数a的取值范围为(　　)

    A．(－2,2)   

    B．(－∞，－2)∪(2，＋∞)

    C．(－∞，－2]∪[2，＋∞)   

    D．[－2,2]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：

    (1)对任意a∈R，a*0＝a；

    (2)对任意a，b∈R，a*b＝ab＋(a*0)＋(b*0)．

    关于函数f(x)＝(ex)*的性质，有如下说法：①函数f(x)的最小值为3；②函数f(x)为偶函数；③函数f(x)的单调递增区间为(－∞，0]．

    其中所有正确说法的个数为(　　)

    A．0                                    B．1 

    C．2                                    D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)的图象向右平移a(a>0)个单位后关于x＝a＋1对称，当x2>x1>1时，[f(x2)－f(x1)](x2－x1)<0恒成立，设a＝f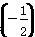，b＝f(2)，c＝f(e)，则a，b，c的大小关系为(　　)

    A．c>a>b                                B．c>b>a 

    C．a>c>b                                D．b>a>c

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)是定义在R上的偶函数，且当x≥0时，f(x)＝2x.若对任意的x∈[a，a＋2]，不等式f(x＋a)≥f2(x)恒成立，则实数a的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列结论中：

    ①函数y＝x(1－2x)(x>0)有最大值；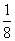

    ②函数y＝2－3x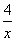－(x<0)有最大值2－4；

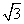    ③若a>0，则(1＋a)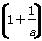≥4.

    正确结论的序号是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设等差数列{an}的前n项和为Sn，已知a1＝2，S6＝22.

    (1)求Sn的表达式；

    (2)若从{an}中抽取一个公比为q的等比数列{akn}，其中k1＝1，且k1<k2<…<kn(kn∈N*)．

    ①当q取最小值时，求{kn}的通项公式；

    ②若关于n(n∈N*)的不等式6Sn>kn＋1有解，试求q的值．

    查看答案和解析>>

    同步练习册答案