
已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列命题:
①若α⊥β,m∥α,则m⊥β;
②若m⊥α,n⊥β,且m⊥n,则α⊥β;
③若m⊥β,m∥α,则α⊥β;
④若m∥α,n∥β,且m∥n,则α∥β.
其中正确命题的序号是( )
A.①④ B.②③
C.②④ D.①③
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
某动点在平面直角坐标系第一象限的整点上运动(含x,y正半轴上的整点),其运动规律为(m,n)→(m+1,n+1)或(m,n)→(m+1,n-1).若该动点从原点出发,经过6步运动到(6,2)点,则有________种不同的运动轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,∠C=90°,∠B=30°,AC=1,M为AB的中点,将△ACM沿CM折起,使A,B间的距离为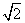 ,如图所示,则M到平面ABC的距离为( )
,如图所示,则M到平面ABC的距离为( )
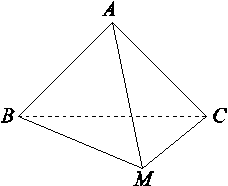
A.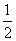 B.
B.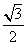 C.1 D.
C.1 D.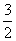
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,底面为直角梯形的四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,E为A1B1的中点,且△ABE为等腰直角三角形,AB∥CD,AB⊥BC,AB=2CD=2BC.
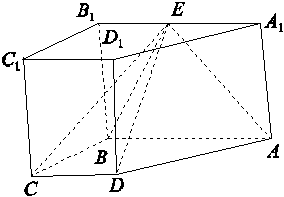
(1)求证:AB⊥DE;
(2)求直线EC与平面ABE所成角的正弦值;
(3)线段EA上是否存在点F,使EC∥平面FBD?若存在,求出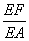 ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f(x)=asin2x+bx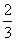 +4(a,b∈R),若f
+4(a,b∈R),若f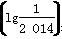 =2 013,则f(lg 2 014)=( )
=2 013,则f(lg 2 014)=( )
A.2 018 B.-2 009 C.2 013 D.-2 013
查看答案和解析>>
科目:高中数学 来源: 题型:
已知g(x)=-x2-4,f(x)为二次函数,满足f(x)+g(x)+f(-x)+g(-x)=0,且f(x)在[-1,2]上的最大值为7,则f(x)=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com