
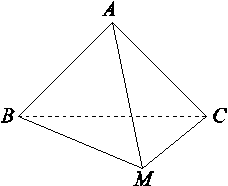
在△ABC中,∠C=90°,∠B=30°,AC=1,M为AB的中点,将△ACM沿CM折起,使A,B间的距离为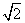 ,如图所示,则M到平面ABC的距离为( )
,如图所示,则M到平面ABC的距离为( )
A.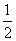 B.
B.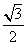 C.1 D.
C.1 D.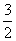
科目:高中数学 来源: 题型:
已知集合M={1,2,3,4,5,6},集合A,B,C为M的非空子集,若∀x∈A,y∈B,z∈C,x<y<z恒成立,则称“A—B—C”为集合M的一个“子集串”,则集合M的“子集串”共有________个.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列命题:
①若α⊥β,m∥α,则m⊥β;
②若m⊥α,n⊥β,且m⊥n,则α⊥β;
③若m⊥β,m∥α,则α⊥β;
④若m∥α,n∥β,且m∥n,则α∥β.
其中正确命题的序号是( )
A.①④ B.②③
C.②④ D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
等边三角形ABC的边长为3,点D,E分别是边AB,AC上的点,且满足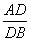 =
=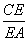 =
=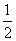 (如图①).将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B为直二面角,连接A1B,A1C(如图②).
(如图①).将△ADE沿DE折起到△A1DE的位置,使二面角A1-DE-B为直二面角,连接A1B,A1C(如图②).
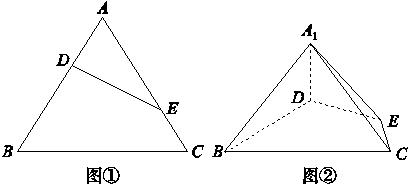
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P,使直线PA1与平面A1BD所成的角为60°?若存在,求出PB的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
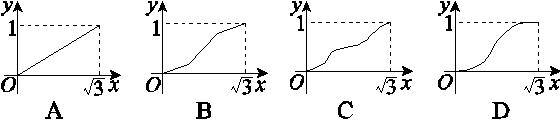
如图,已知正方体ABCD-A1B1C1D1的棱长是1,点E是对角线AC1上一动点,记AE=x(0<x<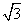 ),过点E平行于平面A1BD的截面将正方体分成两部分,其中点A所在的部分的体积为V(x),则函数y=V(x)的图象大致为( )
),过点E平行于平面A1BD的截面将正方体分成两部分,其中点A所在的部分的体积为V(x),则函数y=V(x)的图象大致为( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com