
 如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 动点A′在平面ABC上的射影在线段AF上 | |
| B. | 恒有平面A′GF⊥平面BCED | |
| C. | 三棱锥A′-EFD的体积有最大值 | |
| D. | 异面直线A′E与BD不可能垂直 |
分析 由斜线的射影定理可判断A正确;由面面垂直的判定定理,可判断B正确;由三棱锥的体积公式,可判断C正确;由异面直线所成的角的概念可判断D不正确
解答 解:∵A′D=A′E,△ABC是正三角形,
∴A′在平面ABC上的射影在线段AF上,故A正确;
由A知,平面A′GF一定过平面BCED的垂线,
∴恒有平面A′GF⊥平面BCED,故B正确;
三棱锥A′-FED的底面积是定值,体积由高即A′到底面的距离决定,
当平面A′DE⊥平面BCED时,三棱锥A′-FED的体积有最大值,故C正确;
当(A′E)2+EF2=(A′F)2时,面直线A′E与BD垂直,故④错误.
故选:D.
点评 本题考查了线面、面面垂直的判定定理、性质定理的运用,考查了空间线线、线面的位置关系及所成的角的概念,考查了空间想象能力


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或4 | B. | 1或4 | C. | 1或2 | D. | -6或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±1 | B. | ±2 | C. | $±\sqrt{2}$ | D. | $±\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
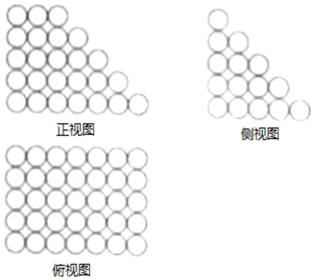 北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n层,上底由长为a个物体,宽为b个物体组成,以下各层的长、宽依次各增加一个物体,最下层成为长为c个物体,宽为d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}[{({2b+d})a+({b+2d})c}]+\frac{n}{6}({c-a})$.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为85.
北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n层,上底由长为a个物体,宽为b个物体组成,以下各层的长、宽依次各增加一个物体,最下层成为长为c个物体,宽为d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}[{({2b+d})a+({b+2d})c}]+\frac{n}{6}({c-a})$.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为85.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $-2\sqrt{3}$ | C. | 0 | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com