
| A. | $-\sqrt{3}$ | B. | $-2\sqrt{3}$ | C. | 0 | D. | $\sqrt{3}$ |
分析 根据正切函数的性质可得其周期T=$\frac{π}{\frac{π}{3}}=3$,依次求出f(1),f(2),f(3),由周期可得f(1)+f(2)+…+f(100)的值.
解答 解:∵f(n)=$tan\frac{nπ}{3}$,
根据正切函数的性质可得其周期T=$\frac{π}{\frac{π}{3}}=3$,
∴f(1)=$\sqrt{3}$,f(2)=$-\sqrt{3}$,f(3)=0.
可得:f(1)=f(2)+f(3)=0.
∴f(1)+f(2)+…+f(100)=33[f(1)+f(2)+f(3)]+f(1)=f(1)=$\sqrt{3}$.
故选:D.
点评 本题主要考查正切函数的图象和性质,周期函数的求和计算.属于基础题


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
 如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,等边△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 动点A′在平面ABC上的射影在线段AF上 | |
| B. | 恒有平面A′GF⊥平面BCED | |
| C. | 三棱锥A′-EFD的体积有最大值 | |
| D. | 异面直线A′E与BD不可能垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 15 | C. | 16 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{2}}{2}$) | B. | (0,$\frac{\sqrt{3}}{3}$) | C. | (0,$\frac{\sqrt{5}}{5}$) | D. | (0,$\frac{\sqrt{6}}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-1,1) | C. | (-1,+∞) | D. | (-3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
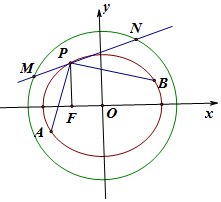 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),离心率为e,椭圆过点P(-2,3)与Q($\frac{2}{e}$,0).
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),离心率为e,椭圆过点P(-2,3)与Q($\frac{2}{e}$,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份200x(年) | 0 | 1 | 2 | 3 | 4 |
| 人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com