
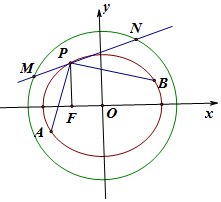
 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),离心率为e,椭圆过点P(-2,3)与Q($\frac{2}{e}$,0).
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),离心率为e,椭圆过点P(-2,3)与Q($\frac{2}{e}$,0).分析 (1)根据椭圆性质列方程解出a,b,c即可得出椭圆方程;
(2)利用垂径定理列方程得出O到直线MN的距离,再根据对称性得出PN;
(3)联立方程组,根据根与系数的关系表示出k1、k2,列方程化简整理得出m.
解答 解:(1)∵椭圆过Q($\frac{2}{e}$,0),∴a=$\frac{2}{e}$=$\frac{2a}{c}$,∴c=2,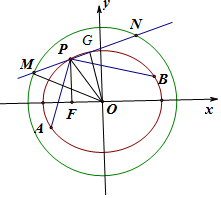
则a2=b2+c2=b2+4,
将P(-2,3)代入椭圆方程:$\frac{{x}^{2}}{{b}^{2}+4}+\frac{{y}^{2}}{{b}^{2}}=1$,
解得:b2=12,a2=16,
∴椭圆的标准方程:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$;
(2)如图,过O作OG⊥MN,垂足为G,设PG=x,
∵OP2=13,OM2=28,PM=PF=3,
∴28-(3+x)2=13-x2,即x=1.
∴PN=PG+GN=PG+PG+PM=2PG+PM=2×1+3=5;
(3)联立方程组$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\end{array}\right.$,消元得:(3+4k2)x2+8kmx+4m2-48=0,
设A(x1,y1),B(x2,y2),则${x}_{1}+{x}_{2}=\frac{-8km}{3+4{k}^{2}},{x}_{1}{x}_{2}=\frac{4{m}^{2}-48}{3+4{k}^{2}}$.
${y}_{1}+{y}_{2}=k({x}_{1}+{x}_{2})+2m=\frac{6m}{3+4{k}^{2}}$,
y1y2=(kx1+m)(kx2+m)=${k}^{2}{x}_{1}{x}_{2}+km({x}_{1}+{x}_{2})+{m}^{2}$=$\frac{3{m}^{2}-48{k}^{2}}{3+4{k}^{2}}$.
又P(-2,3),∴${k}_{1}=\frac{{y}_{1}-3}{{x}_{1}+2}$,${k}_{2}=\frac{{y}_{2}-3}{{x}_{2}+2}$,
∵4k1k2+3=0,∴k1k2=-$\frac{3}{4}$,
即$\frac{{y}_{1}-3}{{x}_{1}+2}•\frac{{y}_{2}-3}{{x}_{2}+2}$=-$\frac{3}{4}$,
即$\frac{{y}_{1}{y}_{2}-3({y}_{1}+{y}_{2})+9}{{x}_{1}{x}_{2}+2({x}_{1}+{x}_{2})+4}$=-$\frac{3}{4}$,
∴4y1y2-12(y1+y2)+36+3x1x2+6(x1+x2)+12=0,
∴12•$\frac{{m}^{2}-16{k}^{2}}{3+4{k}^{2}}$-72•$\frac{m}{3+4{k}^{2}}$+48+12•$\frac{{m}^{2}-12}{3+4{k}^{2}}$-48•$\frac{km}{3+4{k}^{2}}$=0,
整理得:m=2k+3.
点评 本题考查了椭圆的性质,直线与圆,直线与椭圆的位置关系,属于中档题.


科目:高中数学 来源: 题型:填空题
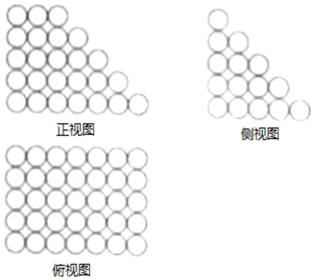 北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n层,上底由长为a个物体,宽为b个物体组成,以下各层的长、宽依次各增加一个物体,最下层成为长为c个物体,宽为d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}[{({2b+d})a+({b+2d})c}]+\frac{n}{6}({c-a})$.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为85.
北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n层,上底由长为a个物体,宽为b个物体组成,以下各层的长、宽依次各增加一个物体,最下层成为长为c个物体,宽为d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}[{({2b+d})a+({b+2d})c}]+\frac{n}{6}({c-a})$.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为85.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $-2\sqrt{3}$ | C. | 0 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{23}{9}$ | B. | -$\frac{20}{31}$ | C. | -6 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com