练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．一件工作可以用2种方法完成，有3人会用第1种方法完成，另外5人会用第2种方法完成，从中选出1人来完成这件工作，不同选法的种数是（　　）
    A．8B．15C．16D．30

    分析 根据题意，分别计算利用选择第1种方法来完成工作和选择第2种方法来完成工作的情况数目，由加法原理计算可得答案．

    解答 解：利用分类计数原理的加法原理：
    （1）选择第1种方法来完成工作的有：3种选法
    （2）选择第2种方法来完成工作的有：5种选法
    所以，有3+5=8种不同的选法；
    故选：A．

    点评 本题考查加法原理的运用，注意分类计数原理与分步计数原理的不同．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知复数z在复平面内对应的点在射线y=2x（x≥0）上，且$|z|=\sqrt{5}$，则复数z的虚部为（　　）
    A．-2B．2C．-1D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F1，F2，过F2作一条直线（不与x轴垂直）与椭圆交于A，B两点，如果△ABF1恰好为等腰直角三角形，该直线的斜率为（　　）
    A．±1B．±2C．$±\sqrt{2}$D．$±\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

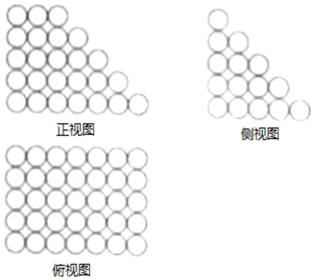    2．北宋数学家沈括的主要数学成就之一为隙积术，所谓隙积，即“积之有隙”者，如累棋、层坛之类，这种长方台形状的物体垛积．设隙积共n层，上底由长为a个物体，宽为b个物体组成，以下各层的长、宽依次各增加一个物体，最下层成为长为c个物体，宽为d个物体组成，沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}[{（{2b+d}）a+（{b+2d}）c}]+\frac{n}{6}（{c-a}）$．已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示，则该垛积中所有小球的个数为85．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．${（x-\frac{2}{{\sqrt{x}}}）^n}$的二项展开式中第五项和第六项的二项式系数最大，则各项的系数和为-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设A={x|x2-4x-5=0}，B={x|x2=1}，则A∪B=（　　）
    A．{-1，1，5}B．{-1，5}C．{1，5}D．{-1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知l1⊥l2，直线l1的倾斜角为60°，则直线l2的倾斜角为（　　）
    A．60°B．120°C．30°D．150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．$若f（n）=tan\frac{nπ}{3}，（n∈{N^*}），则f（1）+f（2）+…+f（100）$=（　　）
    A．$-\sqrt{3}$B．$-2\sqrt{3}$C．0D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．函数f（x）=-2x2+3在点（0，3）处的导数是0．

    查看答案和解析>>

    同步练习册答案