
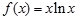 .
. .
. 在区间
在区间 上的最小值;
上的最小值; ,
,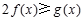 恒成立,求实数
恒成立,求实数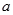 的取值范围;
的取值范围; ,
,  恒成立.
恒成立.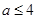 ;(3)见解析.
;(3)见解析.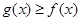 恒成立问题,往往将不等式转化为函数
恒成立问题,往往将不等式转化为函数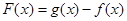 来证明
来证明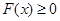 恒成立问题.但有些时候这样转化后不等会乃然很难实现证明,还需对不等式经行恒等变形以达到化简不等式的目的,然后再证.
恒成立问题.但有些时候这样转化后不等会乃然很难实现证明,还需对不等式经行恒等变形以达到化简不等式的目的,然后再证. ,当
,当 ,
,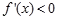 ,
, 单调递减,
单调递减,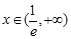 ,
,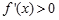 ,
, 单调递增. 1分
单调递增. 1分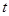 的取值范围不同导致
的取值范围不同导致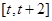 所处的区间函数单调性不同,故对
所处的区间函数单调性不同,故对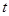 经行分类讨论.)
经行分类讨论.) ,t无解; 2分
,t无解; 2分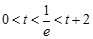 ,即
,即 时,
时,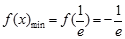 3分
3分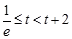 ,即
,即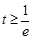 时,
时, 在
在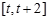 上单调递增,
上单调递增, ;
; 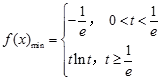 5分
5分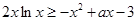 ,则
,则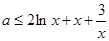 .因对于
.因对于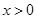 ,
,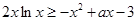 恒成立,故
恒成立,故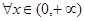 ,
,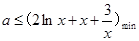
 ,则
,则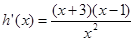 .
.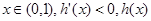 单调递增,
单调递增,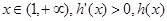 单调递减.
单调递减. ,即
,即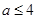 .
. (为了利用第(1)小问结论,并考虑到作差做函数证明不方便,下证
(为了利用第(1)小问结论,并考虑到作差做函数证明不方便,下证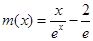 的最值与
的最值与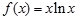 最值的关系.)
最值的关系.)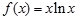 在
在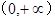 的最小值是
的最小值是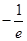 ,当且仅当
,当且仅当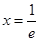 时取到.
时取到.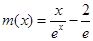 ,则
,则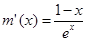 ,易得
,易得 ,当且仅当
,当且仅当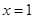 时取到.
时取到. ,都有
,都有 恒成立.
恒成立.

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com