
【题目】某城市一社区接到有关部门的通知,对本社区居民用水量进行调研,通过抽样调查的方法获得了100户居民某年的月均用水量(单位:t),通过分组整理数据,得到数据的频率分布直方图如图所示:
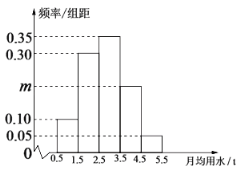
(Ⅰ)求图中m的值;并估计该社区居民月均用水量的中位数和平均值.(保留3位小数)
(Ⅱ)用此样本频率估计概率,若从该社区随机抽查3户居民的月均用水量,问恰有2户超过![]() 的概率为多少?
的概率为多少?
(Ⅲ)若按月均用水量![]() 和
和![]() 分成两个区间用户,按分层抽样的方法抽取10户,每户出一人参加水价调整方案听证会.并从这10人中随机选取3人在会上进行陈述发言,设来自用水量在区间
分成两个区间用户,按分层抽样的方法抽取10户,每户出一人参加水价调整方案听证会.并从这10人中随机选取3人在会上进行陈述发言,设来自用水量在区间![]() 的人数为X,求X的分布列和数学期望.
的人数为X,求X的分布列和数学期望.
【答案】(Ⅰ)![]() ,2.786,2.800;(Ⅱ)0.432;(Ⅲ)分布列见解析,
,2.786,2.800;(Ⅱ)0.432;(Ⅲ)分布列见解析,![]()
【解析】
(Ⅰ)根据频率分布直方图各小矩形面积和为1,即可求得m的值;根据频率分布直方图各小组的频率,由中位数定义即可求解;结合平均数的求法,可用频率分布直方图求得平均数.
(Ⅱ)先求得月均用水量超过![]() 的概率,再结合独立重复试验中概率求法即可得恰有2户超过
的概率,再结合独立重复试验中概率求法即可得恰有2户超过![]() 的概率.
的概率.
(Ⅲ)按照分层抽样,先求得在月均用水量![]() 和
和![]() 在两个区间各自抽取的人数,可知来自用水量在区间
在两个区间各自抽取的人数,可知来自用水量在区间![]() 的人数为X的取值有0,1,2,3,分别求得各自对应的概率即可得分布列,由分布列求得数学期望即可.
的人数为X的取值有0,1,2,3,分别求得各自对应的概率即可得分布列,由分布列求得数学期望即可.
(Ⅰ)由频率分布直方图得:
![]() ,
,
解得![]() ,
,
![]() 的频率为
的频率为![]() ,
,![]() 的频率为0.35,
的频率为0.35,
∴估计该社区居民月均用水量的中位数为:![]()
平均值为:![]() .
.
(Ⅱ)用此样本频率估计概率,从该社区随机抽查3户居民的月均用水量,
月均用水量超过![]() 的概率为:
的概率为:![]() ,
,
∴恰有2户超过![]() 的概率为
的概率为![]() .
.
(Ⅲ)若按月均用水量![]() 和
和![]() 分成两个区间用户,按分层抽样的方法抽取10户,
分成两个区间用户,按分层抽样的方法抽取10户,
月均用水量![]() 中抽取:
中抽取:![]() 户,
户,
月均用水量![]() 中抽取:
中抽取:![]() 户.
户.
从这10人中随机选取3人在会上进行陈述发言,设来自用水量在区间![]() 的人数为X,
的人数为X,
则X的可能取值为0,1,2,3,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
数学期望![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 和
和![]() ,过抛物线
,过抛物线![]() 上一点
上一点![]() 作两条直线与
作两条直线与![]() 分别相切于
分别相切于![]() 两点,分别交抛物线于
两点,分别交抛物线于![]() 两点.
两点.

(1)当![]() 的角平分线垂直
的角平分线垂直![]() 轴时,求直线
轴时,求直线![]() 的斜率;
的斜率;
(2)若直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,例如求1到2000这2000个整数中,能被3除余1且被7除余1的数的个数,现由程序框图,其中MOD函数是一个求余函数,记![]() 表示m除以n的余数,例如
表示m除以n的余数,例如![]() ,则输出i为( ).
,则输出i为( ).
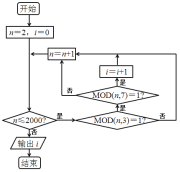
A.98B.97C.96D.95
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (α为参数).以坐标原点O为极点,x轴正半轴为极轴的坐标系中,曲线C2的方程为
(α为参数).以坐标原点O为极点,x轴正半轴为极轴的坐标系中,曲线C2的方程为![]() (m为常数)
(m为常数)
(1)求曲线C1,C2的直角坐标方程;
(2)若曲线C1,C2有两个交点P、Q,当|PQ|![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,抛物线
,抛物线![]() 与圆
与圆![]() 的相交弦长为4.
的相交弦长为4.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)点![]() 为抛物线
为抛物线![]() 的焦点,
的焦点,![]() 为抛物线
为抛物线![]() 上两点,
上两点,![]() ,若
,若![]() 的面积为
的面积为![]() ,且直线
,且直线![]() 的斜率存在,求直线
的斜率存在,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人设计一项单人游戏,规则如下:先将一棋子放在如图所示正方形![]() (边长为2个单位)的顶点
(边长为2个单位)的顶点![]() 处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为
处,然后通过掷骰子来确定棋子沿正方形的边按逆时针方向行走的单位,如果掷出的点数为![]() ,则棋子就按逆时针方向行走
,则棋子就按逆时针方向行走![]() 个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到点
个单位,一直循环下去.则某人抛掷三次骰子后棋子恰好又回到点![]() 处的所有不同走法共有( )
处的所有不同走法共有( )

A. 22种 B. 24种 C. 25种 D. 27种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com