
分析 (Ⅰ)根据M⊆N可讨论M是否为∅:分别求出M=∅和M≠∅时a的取值范围,再求并集便可得出实数a的取值范围;
(Ⅱ)根据条件便知一元二次方程f(x)=0的两个实根为-1,3,从而可以设f(x)=b(x+1)(x-3),带入f(x)+4=0便可得到关于x的一元二次方程,该方程有两个相等实数根,从而△=0,这样即可求出b的值,从而得出f(x)的解析式.
解答 解:(Ⅰ)M⊆N;
(1)若M=∅,则:1-a≥a+1;
∴a≤0;
(2)若M≠∅,则$\left\{\begin{array}{l}{1-a<a+1}\\{1-a≥-1}\\{a+1≤3}\end{array}\right.$;
∴0<a≤2;
∴实数a的取值范围为(-∞,2];
(Ⅱ)f(x)≤0的解集为N={x|-1≤x≤3};
∴f(x)=0的两实根为-1,3;
∴设f(x)=b(x+1)(x-3)=bx2-2bx-3b;
∴bx2-2bx-3b+4=0有两个相等的实数根;
∴△=4b2-4b(4-3b)=0,b≠0;
∴解得b=1;
∴f(x)=x2-2x-3.
点评 考查子集的定义,描述法表示集合,一元二次不等式的解集和对应的一元二次方程实数根的关系,待定系数求函数解析式的方法,以及一元二次方程有两个相等实根时,判别式△的取值情况.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
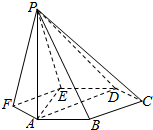 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是(4).
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是(4).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com