
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,其离心率
,其离心率![]() ,点P为椭圆上的一个动点,
,点P为椭圆上的一个动点,![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆的标准方程;
(2)若A,B,C,D是椭圆上不重合的四个点,AC与BD相交于点![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题(1)容易知道当P点为椭圆的上下顶点时,![]() 面积最大,再根据 椭圆的离心率为
面积最大,再根据 椭圆的离心率为![]()
可得到关于a,c的方程组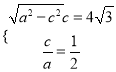 ,解该方程组即可得到a,c,b,从而得出椭圆的方程;(2)先容易求出AC,BD中有一条直线不存在斜率时
,解该方程组即可得到a,c,b,从而得出椭圆的方程;(2)先容易求出AC,BD中有一条直线不存在斜率时![]() ,当直线AC存在斜率k且不为0时,写出直线AC的方程y=k(x+2),联立椭圆的方程消去y得到
,当直线AC存在斜率k且不为0时,写出直线AC的方程y=k(x+2),联立椭圆的方程消去y得到![]() ,根据韦达定理及弦长公式即可求得
,根据韦达定理及弦长公式即可求得![]() ,把k换上
,把k换上![]() 即可得到
即可得到![]() .所以用k表示出
.所以用k表示出 ,这时候设
,这时候设![]() ,t>1,从而得到
,t>1,从而得到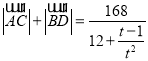 ,根据导数求出
,根据导数求出![]() 的范围,从而求出
的范围,从而求出![]() 的取值范围
的取值范围
试题解析:(1)由题意得,当点![]() 是椭圆的上、下顶点时,
是椭圆的上、下顶点时,![]() 的面积取最大值
的面积取最大值
此时![]()
所以![]()
因为![]()
所以![]() ,
,![]()
所以椭圆方程为![]()
(2)由(1)得椭圆方程为![]() ,则
,则![]() 的坐标为
的坐标为![]()
因为![]() ,所以
,所以![]()
①当直线![]() 与
与![]() 中有一条直线斜率不存在时,易得
中有一条直线斜率不存在时,易得![]()
②当直线![]() 斜率
斜率![]() 存在且
存在且![]() ,则其方程为
,则其方程为![]() ,设
,设![]() ,
,![]()
则点![]() 、
、![]() 的坐标是方程组
的坐标是方程组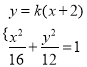 的两组解
的两组解
所以![]()
所以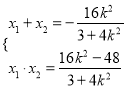
所以![]()
此时直线![]() 的方程为
的方程为![]()
同理由 可得
可得![]()
![]()
令![]() ,则
,则![]() ,
,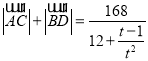
因为![]() ,所以
,所以![]()
所以![]()
综上![]()


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 满足下列两个条件:(1)对任意的
满足下列两个条件:(1)对任意的![]() 恒有
恒有![]() 成立;(2)当
成立;(2)当![]() 时,
时,![]() ;记函数
;记函数![]() ,若函数
,若函数![]() 恰有两个零点,则实数
恰有两个零点,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC中.角A、B、C所对边的长分别为a、b、c满足c=1,![]() 以AB为边向△ABC外作等边三角形△ABD.
以AB为边向△ABC外作等边三角形△ABD.
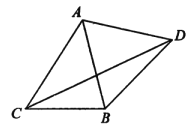
(1)求∠ACB的大小;
(2)设∠ABC=![]() .试求函数
.试求函数![]() 的最大值及
的最大值及![]() 取得最大值时的
取得最大值时的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别是离心率为
分别是离心率为![]() 的椭圆
的椭圆![]() :
:![]() 的左、右焦点,点
的左、右焦点,点![]() 是椭圆
是椭圆![]() 上异于其左、右顶点的任意一点,过右焦点
上异于其左、右顶点的任意一点,过右焦点![]() 作
作![]() 的外角平分线
的外角平分线![]() 的垂线
的垂线![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 在圆
在圆![]() 上,且在第一象限,过
上,且在第一象限,过![]() 作圆
作圆![]() 的切线交椭圆于
的切线交椭圆于![]() 、
、![]() 两点,问:
两点,问:![]() 的周长是否为定值?如果是,求出该定值;如果不是,说明理由.
的周长是否为定值?如果是,求出该定值;如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止供应该厂的生产和生活用水,已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间t(小时,且规定早上6时t=0)的函数关系为:W=100![]() .水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管.
.水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管.
(1)若进水量选择为2级,试问:水塔中水的剩余量何时开始低于10吨?
(2)如何选择进水量,既能始终保证该厂的用水(水塔中水不空)又不会使水溢出?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2-(a-1)x-a<0,a∈R},集合B={x|![]() <0}.
<0}.
(1)当a=3时,求A∩B;
(2)若A∪B=R,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为![]() (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为![]() (m2).
(m2).

(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com