
【题目】已知函数![]() .
.
(1)曲线![]() 在点
在点![]() 处的切线垂直于直线
处的切线垂直于直线![]() :
:![]() ,求
,求![]() 的值;
的值;
(2)若函数![]() 有两个不同的零点,求
有两个不同的零点,求![]() 的范围.
的范围.
【答案】(1)![]() 或
或![]() .(2)
.(2)![]() 或
或![]() .
.
【解析】试题分析:(1)求得![]() ,根据
,根据![]() 在点
在点![]() 处垂直于直线
处垂直于直线![]()
![]() ,得到
,得到
![]() ,即可求解实数
,即可求解实数![]() 的值;
的值;
(2)求得函数![]() 的导函数
的导函数![]() ,可分
,可分![]() 、
、![]() 和
和![]() 三种情况讨论,由函数
三种情况讨论,由函数![]() 有两个不同的零点,列出不等式,即可求解
有两个不同的零点,列出不等式,即可求解![]() 的取值范围.
的取值范围.
试题解析:
(1)![]() ,
,
因为![]() 在点
在点![]() 处垂直于直线
处垂直于直线![]()
![]() ,
,
所以![]() ,
,![]() ,解得
,解得![]() 或
或![]() .
.
(2)函数![]() 的定义域为
的定义域为![]() ,
,![]() .
.
①当![]() 时,
时,![]()
![]() ,无零点;
,无零点;
②当![]() 时,
时,![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
∴![]() .
.
因为![]() ,
,
且当![]() 时,
时,![]() ,当
,当![]() →
→![]() 时,
时,![]() ,
,![]() ,
,
∴若函数![]() 有两个不同的零点,需
有两个不同的零点,需![]() ,即
,即![]() ,
,![]() ;
;
③当![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
∴![]() .
.
当![]() →
→![]() 和当
和当![]() →
→![]() ,均有
,均有![]() ,
,
若函数![]() 有两个不同的零点,需
有两个不同的零点,需![]() 时,即
时,即![]() ,
,![]() .
.
综上,函数![]() 有两个不同的零点,
有两个不同的零点,![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下:

附:![]() 的观测值
的观测值
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,其离心率
,其离心率![]() ,点P为椭圆上的一个动点,
,点P为椭圆上的一个动点,![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆的标准方程;
(2)若A,B,C,D是椭圆上不重合的四个点,AC与BD相交于点![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用![]() 列联表,由计算可得
列联表,由计算可得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的反函数,定义:若对于给定实数
的反函数,定义:若对于给定实数![]() ,函数
,函数![]() 与
与![]() )互成反函数,则称
)互成反函数,则称![]() 满足“
满足“![]() 和性质”,若函数
和性质”,若函数![]() 与
与![]() 互为反函数,则称
互为反函数,则称![]() 满足
满足![]() 积性质
积性质
(1)判断函数![]() 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由;
(2)求所有满足“2和性质”的一次函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,判断函数
,判断函数![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)若函数![]() 在
在![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围;
的取值范围;
(3)若存在实数![]() 使得关于
使得关于![]() 的方程
的方程![]() 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从高三学生中抽取![]() 名学生参加数学竞赛,成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间
名学生参加数学竞赛,成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间![]() ,且成绩在区间
,且成绩在区间![]() 的学生人数是
的学生人数是![]() 人.
人.

(1)求![]() ,
,![]() 的值;
的值;
(2)若从数学成绩(单位:分)在![]() 的学生中随机选取
的学生中随机选取![]() 人进行成绩分析.
人进行成绩分析.
①列出所有可能的抽取结果;
②设选取的![]() 人中,成绩都在
人中,成绩都在![]() 内为事件
内为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义在[0,2]上的增函数,且图像是连续不断的曲线,若f(0)=M,f(2)=N(M>0,N>0),那么下列四个命题中是真命题的有( )
A.必存在x∈[0,2],使得f(x)![]() B.必存在x∈[0,2],使得f(x)
B.必存在x∈[0,2],使得f(x)![]()
C.必存在x∈[0,2],使得f(x)![]() D.必存在x∈[0,2],使得f(x)
D.必存在x∈[0,2],使得f(x)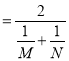
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com