练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．设i是虚数单位，则复数$\frac{2i}{1+i}$在复平面内所对应的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    分析 直接由复数代数形式的乘除运算化简复数$\frac{2i}{1+i}$，求出复数$\frac{2i}{1+i}$在复平面内所对应的点的坐标，则答案可求．

    解答 解：由$\frac{2i}{1+i}$=$\frac{2i（1-i）}{（1+i）（1-i）}=1+i$，
    则复数$\frac{2i}{1+i}$在复平面内所对应的点的坐标为：（1，1），位于第一象限．
    故选：A．

    点评 本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=$\sqrt{lo{g}_{\frac{1}{3}}（x-2）}$的定义域为A，函数g（x）=（$\frac{1}{2}$）x（x≥-2）的值域为B．
    （1）求（∁RA）∩B；
    （2）若集合C={x|a≤x≤2a-2}且A∩C=C，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若函数f（x）=$\left\{\begin{array}{l}{{a}^{x-a}，x≤a}\\{-{x}^{2}+2ax-{a}^{2}+2a，x＞a}\end{array}\right.$（a＞0且a≠1）在其定义域内单调，则实数a的取值范围为（　　）
    A．（0，$\frac{1}{2}$）B．（0，$\frac{1}{2}$]C．（$\frac{1}{2}$，1）D．[$\frac{1}{2}$，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．直线y=a分别与函数y=4x+4和y=3x+lnx的图象相交于M、N两点，则|MN|的最小值为（　　）
    A．5B．1C．$\frac{5}{4}$D．$\frac{3}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

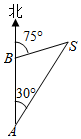    4．如图，一艘船下午13：30在A处测得灯塔S在它的北偏东30°处，之后它继续沿正北方向匀速航行，14：00到达B处，此时又测得灯塔S在它的北偏东75°处，且与它相距9$\sqrt{2}$海里，则此船的航速为36海里/小时．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

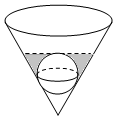    14．祖暅，字景烁，祖冲之之子，南北朝时代的伟大科学家．祖暅在数学上有突出的贡献，他在实践的基础上，于5世纪末提出下面的计算原理：祖暅原理：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等，请同学们用祖暅原理解决如下问题：如图，有一个倒圆锥形容器，它的轴截面是一个正三角形，在容器内放一个半径为r的铁球，再注入水，使水面与球正好相切（而且球与倒圆锥相切效果很好，水不能流到倒圆锥容器底部），然后将球取出，则这时容器中水的深度为$\root{3}{15}$r．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=ex+ax-1（a∈R）．
    （1）求函数f（x）的单调区间；
    （2）记函数f（x）的导数为f′（x），证明：对任意a∈R，给定x1，x2且x1＜x2存在x0∈（x1，x2），使得f′（x0）=$\frac{f（{x}_{2}）-f（{x}_{1}）}{{x}_{2}-{x}_{1}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-2，x）．
    （1）当$\overrightarrow{a}$⊥$\overrightarrow{b}$时，求x的值；
    （2）若x=$\frac{1}{2}$，求|$\overrightarrow{a}$+2$\overrightarrow{b}$|．

    查看答案和解析>>

    科目：高中数学 来源：2016-2017学年内蒙古高二文上月考一数学试卷（解析版） 题型：选择题

    已知双曲线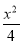-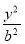=1的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于（ ）

    A.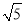 B.4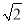 C.3 D.5

    查看答案和解析>>

    同步练习册答案