
分析 (1)求出函数的导数,问题转化为$x+\frac{1}{x}+1-a<0$有解,根据不等式的性质求出a的范围即可;
(2)求出函数的导数,得到f(x1)-f(x2)=$ln\frac{x_1}{x_2}+\frac{1}{2}({\frac{x_1^2-x_2^2}{{{x_1}{x_2}}}})=ln\frac{x_1}{x_2}+\frac{1}{2}({\frac{x_1}{x_2}-\frac{x_2}{x_1}})$,设$t=\frac{x_1}{x_2},t>1$,令$h(t)=lnt-\frac{1}{2}({t-\frac{1}{t}}),t>1$,根据函数的单调性求出函数的极大值即可.
解答 解:(1)∵$f(x)=lnx+\frac{1}{2}{x^2}-({a-1})x$,
∴$f'(x)=\frac{1}{x}+x({a-1})=\frac{{{x^2}-({a-1})x+1}}{x},x>0$,
由题意知f'(x)<0在(0,+∞)上有解,
即$x+\frac{1}{x}+1-a<0$有解,
∵x>0,∴$x+\frac{1}{x}≥2$,当且仅当x=1时等号成立,
要使$x+\frac{1}{x}<a-1$有解,
只需要$x+\frac{1}{x}$的最小值小于a-1,
∴2<a-1,解得实数a的取值范围是{a|a>3}.
(2)∵$f(x)=lnx+\frac{1}{2}{x^2}-({a-1})x$,
∴$f'(x)=\frac{1}{x}+x-({a-1})=\frac{{{x^2}-({a-1})x+1}}{x},x>0$,
由题意知f'(x)=0在(0,+∞)上有解,
∵x>0,设μ(x)=x2-(a-1)x+1,又$a≥\frac{7}{2}$,
∴△=(a-1)2-4>0,∴x1+x2=a-1,x1x2=1,
则$f({x_1})-f({x_2})=[{ln{x_1}+\frac{1}{2}x_1^2-({a-1}){x_1}}]-[{ln{x_2}+\frac{1}{2}x_2^2-({a-1}){x_2}}]$
=$ln\frac{x_1}{x_2}+\frac{1}{2}({x_1^2+x_2^2})-({a-1})({{x_1}-{x_2}})=ln\frac{x_1}{x_2}+\frac{1}{2}({x_1^2-x_2^2})-({{x_1}+{x_2}})({{x_1}-{x_2}})$
=$ln\frac{x_1}{x_2}+\frac{1}{2}({\frac{x_1^2-x_2^2}{{{x_1}{x_2}}}})=ln\frac{x_1}{x_2}+\frac{1}{2}({\frac{x_1}{x_2}-\frac{x_2}{x_1}})$,
∵x1>x2>0,所以设$t=\frac{x_1}{x_2},t>1$,
令$h(t)=lnt-\frac{1}{2}({t-\frac{1}{t}}),t>1$,则$h'(t)=\frac{1}{t}-\frac{1}{2}({1+\frac{1}{t}})=-\frac{{{{({t-1})}^2}}}{{2{t^2}}}<0$,
∴h(t)在(1,+∞)上单调递减,
∵$a≥\frac{7}{2}$,∴${({a-1})^2}≥\frac{25}{4}$,∴${({a-1})^2}={({{x_1}+{x_2}})^2}=\frac{{{{({{x_1}+{x_2}})}^2}}}{{{x_1}{x_2}}}=t+\frac{1}{t}+2≥\frac{25}{4}$,
∵t>1,∴由4t2-17t+4=(4t-1)(t-4)≥0,得t≥4,
∴$h(t)≤h(4)=ln4-\frac{1}{2}({4-\frac{1}{4}})=2ln2-\frac{15}{8}$,
故f(x1)-f(x2)的最大值为$2ln2-\frac{15}{8}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及换元思想,转化思想,考查不等式的性质,是一道综合题.


科目:高中数学 来源: 题型:解答题
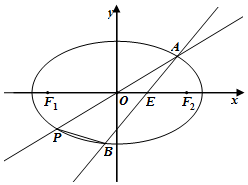 如图,在平面直角坐标系xoy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{\sqrt{6}}{3}$,a=$\sqrt{6}$,直线l与x轴交于点E,与椭圆C交于A、B两点.
如图,在平面直角坐标系xoy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{\sqrt{6}}{3}$,a=$\sqrt{6}$,直线l与x轴交于点E,与椭圆C交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{10}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com