
分析 (1)利用三角函数的诱导公式化简,再化弦为切得答案;
(2)化切为弦,再由两角差的余弦变形,进一步利用倍角公式化简得答案.
解答 解:(1)∵tanα=2,
∴$\frac{sin(2π-α)+cos(π+α)}{{cos(α-π)-cos(\frac{3π}{2}-α)}}$=$\frac{-sinα-cosα}{-cosα+sinα}=\frac{-tanα-1}{-1+tanα}=-3$;
(2)$sin50°(1+\sqrt{3}tan10°)$=$\frac{sin50°(cos10°+\sqrt{3}sin10°)}{cos10°}$=$\frac{{2sin{{50}°}cos{{50}°}}}{{cos{{10}°}}}=\frac{{sin{{100}°}}}{{cos{{10}°}}}=\frac{{cos{{10}°}}}{{cos{{10}°}}}=1$.
点评 本题考查三角函数的化简求值,考查了诱导公式、同角三角函数基本关系式、两角和与差的余弦及倍角公式的应用,是基础的计算题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
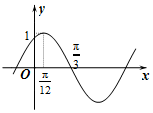 $f(x)=Asin(ωx+φ)(A>0,|φ|<\frac{π}{2})$的图象如图所示,为了得到f(x)的图象,则只要将g(x)=cos2x的图象( )
$f(x)=Asin(ωx+φ)(A>0,|φ|<\frac{π}{2})$的图象如图所示,为了得到f(x)的图象,则只要将g(x)=cos2x的图象( )| A. | 向右平移$\frac{π}{12}$个单位长度 | B. | 向右平移$\frac{π}{6}$个单位长度 | ||
| C. | 向左平移$\frac{π}{12}$个单位长度 | D. | 向左平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
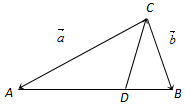
| A. | $\overrightarrow{DC}=-\frac{5}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | B. | $\overrightarrow{DC}$=$-\frac{1}{2}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | C. | $\overrightarrow{DC}$=$-\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | D. | $\overrightarrow{DC}=-\frac{1}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com