
分析 (Ⅰ)求出z1+z2,根据纯虚数的定义求出m的值即可;
(Ⅱ)求出$\overline{{z}_{2}}$,从而求出z1•$\overline{z_2}$的值.
解答 解:(Ⅰ)${z_1}+{z_2}=({m^2}+2m-3)+(\frac{1}{m+1}+\frac{1}{2})i$,
∵z1+z2是纯虚数,
∴$\left\{\begin{array}{l}{m^2}+2m-3=0\\ \frac{1}{m+1}+\frac{1}{2}≠0\end{array}\right.$,
则m=1;
(Ⅱ)由(Ⅰ)得${z_1}=1+\frac{1}{2}i$,${z_2}=-1+\frac{1}{2}i$,
则$\overline{z_2}=-1-\frac{1}{2}i$,
∴${z_1}•\overline{z_2}=(1+\frac{1}{2}i)(-1-\frac{1}{2}i)$=$-{(1+\frac{1}{2}i)^2}$=$-(\frac{3}{4}+i)$=$-\frac{3}{4}-i$.
点评 本题主要考查复数的有关概念及四则运算等基本知识.考查概念识记、运算化简能力.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:选择题
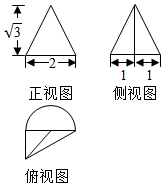
| A. | 4+$\frac{3π}{2}$ | B. | 4+3π | C. | 4+π | D. | 4+$\sqrt{3}$+$\frac{3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 和$\frac{1}{2}$ | B. | 15和$\frac{1}{4}$ | C. | 18和$\frac{2}{3}$ | D. | 20和$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n=4,p=0.6 | B. | n=6,p=0.4 | C. | n=8,p=0.3 | D. | n=24,p=0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
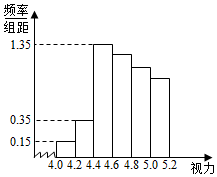 某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.| 年级名次 是否近视 | 前50名 | 后50名 |
| 近视 | 42 | 34 |
| 不近视 | 8 | 16 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com