
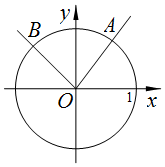
 如图,在平面直角坐标系xOy中,角α是以Ox轴为始边,OA为终边的角,把OA绕点O逆时针旋转β(0<β<π)角到OB位置,已知A、B是单位圆上分别位于第一、二象限内的点,它们的横坐标分别为$\frac{3}{5}$、-$\frac{{\sqrt{2}}}{2}$.
如图,在平面直角坐标系xOy中,角α是以Ox轴为始边,OA为终边的角,把OA绕点O逆时针旋转β(0<β<π)角到OB位置,已知A、B是单位圆上分别位于第一、二象限内的点,它们的横坐标分别为$\frac{3}{5}$、-$\frac{{\sqrt{2}}}{2}$.分析 (1)由已知求出A、B的坐标,由三角函数的定义求得sinα、cosα的值,利用倍角公式化简$\frac{1+sin2α}{cos2α}$后求值;
(2)由三角函数的定义求出sin(α+β)与cos(α+β)的值,再由cosβ═cos[(α+β)-α]展开两角差的余弦求解.
解答 解:(1)由已知可得点A的坐标为($\frac{3}{5}$,$\frac{4}{5}$),点B的坐标为(-$\frac{{\sqrt{2}}}{2}$,$\frac{{\sqrt{2}}}{2}$),
∴$sinα=\frac{4}{5}$,$cosα=\frac{3}{5}$,
则$\frac{1+sin2α}{cos2α}$=$\frac{(sinα+cosα)^{2}}{(cosα+sinα)(cosα-sinα)}$=$\frac{sinα+cosα}{cosα-sinα}$=$\frac{\frac{4}{5}+\frac{3}{5}}{\frac{3}{5}-\frac{4}{5}}$=-7;
(2)$sin(α+β)=\frac{{\sqrt{2}}}{2}$,$cos(α+β)=-\frac{{\sqrt{2}}}{2}$,且β=(α+β)-α,
∴cosβ═cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=$-\frac{\sqrt{2}}{2}×\frac{3}{5}+\frac{\sqrt{2}}{2}×\frac{4}{5}$=$\frac{{\sqrt{2}}}{10}$.
点评 本题考查任意角的三角函数的定义,考查了两角差的余弦,关键是“拆角配角”思想的应用,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{{\sqrt{10}}}{4}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{17}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2<b2 | B. | a2b<ab2 | C. | D.$\frac{1}{a}$>$\frac{1}{b}$ | D. | 2a-2b<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 经过两条平行直线,有且只有一个平面 | |
| B. | 如果两条直线平行于同一个平面,那么这两条直线平行 | |
| C. | 三点确定唯一一个平面 | |
| D. | 如果一个平面内不共线的三个点到另一平面的距离相等,则这两个平面相互平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com