
【题目】已知函数![]() .
.
(1)求函数![]() 在
在![]() 上的单调递增区间;
上的单调递增区间;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,再将图象上所有点的横坐标伸长到原来的
个单位长度,再将图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象.求证:存在无穷多个互不相同的整数
的图象.求证:存在无穷多个互不相同的整数![]() ,使得
,使得![]() .
.
【答案】(1)单调递增区间为![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)利用二倍角的降幂公式以及辅助角公式可将函数![]() 的解析式化简为
的解析式化简为![]() ,然后求出函数
,然后求出函数![]() 在
在![]() 上的单调递增区间
上的单调递增区间![]() ,与定义域取交集可得出答案;
,与定义域取交集可得出答案;
(2)利用三角函数图象变换得出![]() ,解出不等式
,解出不等式![]() 的解集
的解集![]() ,可得知对
,可得知对![]() 中的任意一个
中的任意一个![]() ,每个区间
,每个区间![]() 内至少有一个整数
内至少有一个整数![]() 使得
使得![]() ,从而得出结论.
,从而得出结论.
(1)![]()
![]() .
.
令![]() ,解得
,解得![]() ,
,
所以,函数![]() 在
在![]() 上的单调递增区间为
上的单调递增区间为![]() ,
,
![]() ,因此,函数
,因此,函数![]() 在
在![]() 上的单调递增区间为
上的单调递增区间为![]() ;
;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,
的图象,
再将图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象,
的图象,
由![]() ,
,
对于![]() 中的任意一个
中的任意一个![]() ,区间
,区间![]() 长度始终为
长度始终为![]() ,大于
,大于![]() ,
,
![]() 每个区间
每个区间![]() 至少含有一个整数,
至少含有一个整数,
因此,存在无穷多个互不相同的整数![]() ,使得
,使得![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知一动圆经过点
中,已知一动圆经过点![]() 且在
且在![]() 轴上截得的弦长为4,设动圆圆心的轨迹为曲线
轴上截得的弦长为4,设动圆圆心的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,
,![]() ,
,![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点
两点![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,求证:直线
,求证:直线![]() 过定点
过定点![]() ,并求出定点
,并求出定点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75],按上述分组方法得到的频率分布直方图如图所示.因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若前两组的学生中体育生有8名.
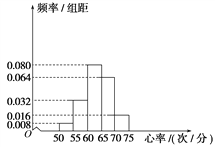
(1)根据频率分布直方图及题设数据完成下列2×2列联表.
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计50 |
(2)根据(1)中表格数据计算可知,________(填“有”或“没有”)99.5%的把握认为“心率小于60次/分与常年进行系统的身体锻炼有关”.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 的奇函数
的奇函数![]() 满足:①
满足:①![]() ;②对任意
;②对任意![]() 均有
均有![]() ;③对任意
;③对任意![]() ,均有
,均有![]() .
.
(1)求![]() 的值;
的值;
(2)利用定义法证明![]() 在
在![]() 上单调递减;
上单调递减;
(3)若对任意![]() ,恒有
,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在同一直角坐标系中,经过伸缩变换 后,曲线C的方程变为
后,曲线C的方程变为![]() .以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线/的极坐标方程为
.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线/的极坐标方程为![]() .
.
(1)求曲线C和直线l的直角坐标方程;
(2)过点![]() 作l的垂线l0交C于A,B两点,点A在x轴上方,求
作l的垂线l0交C于A,B两点,点A在x轴上方,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在黄陵中学举行的数学知识竞赛中,将高二两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.

(1)求第二小组的频率;
(2)求这两个班参赛的学生人数是多少?
(3)这两个班参赛学生的成绩的中位数应落在第几小组内?(不必说明理由)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .不过原点的直线
.不过原点的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,设直线
两点,设直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() 成等比数列.
成等比数列.
(1)求![]() 的值;
的值;
(2)若点![]() 在椭圆
在椭圆![]() 上,满足
上,满足![]() 的直线
的直线![]() 是否存在?若存在,求出直线
是否存在?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com