
���� ͨ�����η��õ�|F1C|=|CO|=$\frac{1}{2}$����$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-1}=1}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$���ɵõ�A�����꣬�Ӷ����OA��б�ʣ���ֱ��ABб��Ϊ0��k��$\frac{\sqrt{3}}{3}$�����a��ȡֵ��Χ���Ӷ����e��ȡֵ��Χ��
��� �⣺���߶�MN��x�ύ��ΪC��
AF1���е�ΪM��BF1���е�ΪN��
��MN��AB��|F1C|=|CO|=$\frac{1}{2}$��
��A��BΪ��Բ�Ϲ���ԭ��ԳƵ����㣬
��|CM|=|CN|��
��ԭ��O�����߶�MNΪֱ����Բ�ϣ�
��|CO|=|CM|=|CN|=$\frac{1}{2}$��
��|OA|=|OB|=c=1��
��|OA|��b��
��a2=b2+c2��2c2��
��e=$\frac{c}{a}$��$\frac{\sqrt{2}}{2}$��
��A��x��y����
��$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-1}=1}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$��
��$\left\{\begin{array}{l}{{x}^{2}={a}^{2}��2-{a}^{2}��}\\{{y}^{2}=1-2{a}^{2}+{a}^{4}}\end{array}\right.$��
��ֱ��ABб��Ϊ0��k��$\frac{\sqrt{3}}{3}$��
��0��$\frac{1-2{a}^{2}+{a}^{4}}{{a}^{2}��2-{a}^{2}��}$��$\frac{1}{3}$��
��$\frac{1}{2}$��a2��$\frac{3}{2}$��
��Ϊ$\frac{\sqrt{2}}{2}$��a��$\frac{\sqrt{6}}{2}$��
��e=$\frac{c}{a}$=$\frac{1}{a}$��[$\frac{\sqrt{6}}{3}$��$\sqrt{2}$]��
����0��e��1��
��������e��ȡֵ��ΧΪ[$\frac{\sqrt{6}}{3}$��1����
�ʴ�Ϊ��[$\frac{\sqrt{6}}{3}$��1����
���� ���⿼����Բ�ķ��̺����ʣ���Ҫ������Բ���̵����ã�ͬʱ����Բ�����ʺ�ֱ��б�ʹ�ʽ�����ã��������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1008 | B�� | 0 | C�� | 2016 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
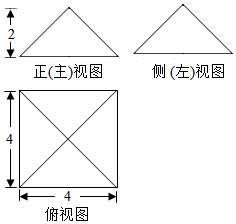
| A�� | $\frac{16}{3}$ | B�� | 16 | C�� | 32 | D�� | $\frac{32}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
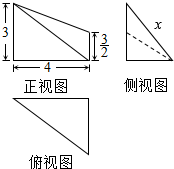 ij�����������ͼ��ͼ��ʾ�����ü���������Ϊ3$\sqrt{7}$�������ͼ���߶εij���x��ֵ�ǣ�������
ij�����������ͼ��ͼ��ʾ�����ü���������Ϊ3$\sqrt{7}$�������ͼ���߶εij���x��ֵ�ǣ�������| A�� | 5 | B�� | 4 | C�� | 2$\sqrt{7}$ | D�� | $\sqrt{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
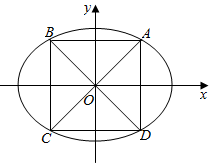 ��ͼ����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������Բ�ij��᳤Ϊ8��������Ϊ$\frac{\sqrt{7}}{4}$��
��ͼ����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������Բ�ij��᳤Ϊ8��������Ϊ$\frac{\sqrt{7}}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��0 | B�� | 0��a��1 | C�� | a��1 | D�� | a��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=cosx�ڵڶ������Ǽ����� | B�� | y=tanx�ڶ��������������� | ||
| C�� | y=|cos��2x+$\frac{��}{3}$��|��������$\frac{��}{2}$ | D�� | y=sin|x|������Ϊ2�е�ż���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com