
分析 (1)(2)根据指数的基本运算法则求解即可.
解答 解:${y_1}={a^{3x+1}}$,${y_2}={a^{-2x}}$,其中若a>0且a≠1,
(1)y1=y2,即a3x+1=a-2x,
可得:3x+1=-2x,
解得:x=$\frac{1}{5}$.
∴当x=$\frac{1}{5}$时,y1=y2;
(2)y1<y2.即a3x+1<a-2x,
当a>1时,可得:3x+1<-2x,
解得:x<$\frac{1}{5}$.
当1>a>0时,可得:3x+1>-2x,
解得:x>$\frac{1}{5}$.
综上:当a>1时,x<$\frac{1}{5}$.
当1>a>0时,x>$\frac{1}{5}$.
点评 本题主要考查了指数的基本运算法和底数的讨论思想.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 28 | C. | 40 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
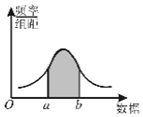
| A. | 组距越大,频率分布折线图越接近于它 | |
| B. | 样本容量越小,频率分布折线图越接近于它 | |
| C. | 阴影部分的面积代表总体在(a,b)内取值的百分比 | |
| D. | 阴影部分的平均高度代表总体在(a,b)内取值的百分比 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | (-1)n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
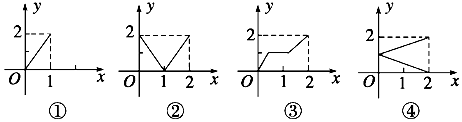
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{5}$ | C. | -$\frac{5\sqrt{3}}{3}$ | D. | -$\frac{3\sqrt{3}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第四象限 | B. | 第一象限 | C. | 第三象限 | D. | 第二象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com