
分析 (Ⅰ)由题意画出简图,由CD方程求出斜率,得到AB所在直线的斜率,得到AB所在直线方程,联立AB、BE的方程求得B的坐标;
(Ⅱ)设出C的坐标,把C的坐标代入CD方程,再由中点坐标公式求出AC中点E的坐标,把E的坐标代入BE方程,联立方程组求出C的坐标,再由直线方程的两点式得答案.
解答 解:(Ⅰ)如图,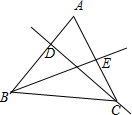
由AB边上的高CD所在的直线方程为:x+y-2=0,得kCD=-1,则kAB=1,
又A(1,-2),∴AB:y+2=1×(x-1),即x-y-3=0.
联立$\left\{\begin{array}{l}{x+y-2=0}\\{2x-y+3=0}\end{array}\right.$,解得B(-6,-9);
(Ⅱ)设C(m,n),则m+n-2=0,
AC中点E($\frac{m+1}{2},\frac{n-2}{2}$),则$2×\frac{m+1}{2}-\frac{n-2}{2}-2=0$,即2m-n=0.
联立$\left\{\begin{array}{l}{2m-n=0}\\{m+n-2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{2}{3}}\\{n=\frac{4}{3}}\end{array}\right.$,∴C($\frac{2}{3},\frac{4}{3}$).
∴AC所在直线方程为$\frac{y+2}{\frac{4}{3}+2}=\frac{x-1}{\frac{2}{3}-1}$,即10x+y-8=0.
点评 本题考查直线的方程的求法,考查两直线位置关系及中点坐标公式的应用,是中档题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 以三个向量所在线段为棱一定可以作一个平行六面体 | |
| B. | 设平行六面体的三条棱为$\overrightarrow{AB}$,$\overrightarrow{A{A}_{1}}$,$\overrightarrow{AD}$所在线段,则这一平行六面体的体对角线所对应的向量是$\overrightarrow{AB}$+$\overrightarrow{A{A}_{1}}$+$\overrightarrow{AD}$ | |
| C. | 若$\overrightarrow{OP}$=$\frac{1}{2}$($\overrightarrow{PA}$+$\overrightarrow{PB}$)成立,则点P一定是线段AB的中点 | |
| D. | 在空间中,若$\overrightarrow{AB}$与$\overrightarrow{CD}$是共线向量,则A,B,C,D四点共面 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
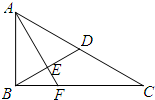 如图,△ABC中,∠ABC=90°,∠C=30°,AB=1,D为AC中点,AE⊥BD于点E,延长AE交BC于点F,沿BD将△ABC折成四面体A-BCD.
如图,△ABC中,∠ABC=90°,∠C=30°,AB=1,D为AC中点,AE⊥BD于点E,延长AE交BC于点F,沿BD将△ABC折成四面体A-BCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{5}$ | D. | $2\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
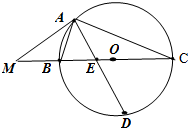 如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点M,∠BAC的平分线分别交圆O和BC于点D,E,若MA=$\frac{5}{2}$MB=15.
如图,△ABC内接于直径为BC的圆O,过点A作圆O的切线交CB的延长线于点M,∠BAC的平分线分别交圆O和BC于点D,E,若MA=$\frac{5}{2}$MB=15.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 人如图,在四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,∠BAD=60°,AB=2AD,AP⊥BD.
人如图,在四棱锥P-ABCD中,底面ABCD是梯形,AB∥CD,∠BAD=60°,AB=2AD,AP⊥BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com