
【题目】[选修4-4:参数方程与极坐标系]
已知曲线C1的参数方程为 ![]() (t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为 ![]() .
.
(Ⅰ)求曲线C2的直角坐标系方程;
(Ⅱ)设M1是曲线C1上的点,M2是曲线C2上的点,求|M1M2|的最小值.
【答案】(Ⅰ)解:由ρ= ![]() 可得ρ=x+2,∴ρ2=(x+2)2①,
可得ρ=x+2,∴ρ2=(x+2)2①,
∵x=ρcosθ,y=ρsinθ,
∴x2+y2=ρ(cos2θ+sin2θ)=ρ2②
由①②两式子可得
y2=4(x+1);
(Ⅱ)曲线C1的参数方程为 ![]() (t为参数),消去t得:2x+y+4=0.
(t为参数),消去t得:2x+y+4=0.
∴曲线C1的直角坐标方程为2x+y+4=0.
∵M1是曲线C1上的点,M2是曲线C2上的点,
∴|M1M2|的最小值等于M2到直线2x+y+4=0的距离的最小值.
设M2(r2﹣1,2r),M2到直线2x+y+4=0的距离为d,
则d=  =
= 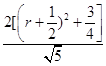 ≥
≥ ![]() .
.
∴|M1M2|的最小值为 ![]() .
.
【解析】(Ⅰ)把 ![]() 变形,得到ρ=ρcosθ+2,结合x=ρcosθ,y=ρsinθ得答案;
变形,得到ρ=ρcosθ+2,结合x=ρcosθ,y=ρsinθ得答案;
(Ⅱ)由 ![]() (t为参数),消去t得到曲线C1的直角坐标方程为2x+y+4=0,由M1是曲线C1上的点,M2是曲线C2上的点,把|M1M2|的最小值转化为M2到直线2x+y+4=0的距离的最小值.设M2(r2﹣1,2r),然后由点到直线的距离公式结合配方法求解.
(t为参数),消去t得到曲线C1的直角坐标方程为2x+y+4=0,由M1是曲线C1上的点,M2是曲线C2上的点,把|M1M2|的最小值转化为M2到直线2x+y+4=0的距离的最小值.设M2(r2﹣1,2r),然后由点到直线的距离公式结合配方法求解.


科目:高中数学 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如表: 
表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推,例如6613用算筹表示就是: ![]() ,则5288用算筹式可表示为 .
,则5288用算筹式可表示为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆C: ![]() =1(a>b>0),称圆心在原点O,半径为
=1(a>b>0),称圆心在原点O,半径为 ![]() 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F( ![]() ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为 ![]() .
.
(Ⅰ)求椭圆C的方程和其“准圆”方程;
(Ⅱ)点P是椭圆C的“准圆”上的动点,过点P作椭圆的切线l1 , l2交“准圆”于点M,N.
(ⅰ)当点P为“准圆”与y轴正半轴的交点时,求直线l1 , l2的方程并证明l1⊥l2;
(ⅱ)求证:线段MN的长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn , Sn=(2n﹣1)an , 且a1=1.
(1)求数列{an}的通项公式;
(2)若bn=nan , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1= ![]() ,an+1=10an+1.
,an+1=10an+1.
(1)证明数列{an+ ![]() }是等比数列,并求数列{an}的通项公式;
}是等比数列,并求数列{an}的通项公式;
(2)数列{bn}满足bn=lg(an+ ![]() ),Tn为数列{
),Tn为数列{ ![]() }的前n项和,求证:Tn<
}的前n项和,求证:Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的四边形ABCD中,∠BAD=90°,∠BCD=120°,∠BAC=60°,AC=2,记∠ABC=θ.
(Ⅰ)求用含θ的代数式表示DC;
(Ⅱ)求△BCD面积S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在正常数a,b,使得x∈R有f(x+a)≤f(x)+b恒成立,则称f(x)为“限增函数”.给出下列三个函数:①f(x)=x2+x+1;② ![]() ;③f(x)=sin(x2),其中是“限增函数”的是( )
;③f(x)=sin(x2),其中是“限增函数”的是( )
A.①②③
B.②③
C.①③
D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P在圆C:x2+y2=4上,而Q为P在x轴上的投影,且点N满足 ![]() ,设动点N的轨迹为曲线E.
,设动点N的轨迹为曲线E.
(1)求曲线E的方程;
(2)若A,B是曲线E上两点,且|AB|=2,O为坐标原点,求△AOB的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com