
分析 (1)根据已知中f(x)=x3+ax2+bx+1,我们根据求函数导函数的公式,易求出导数f'(x),结合f'(1)=2a,f'(2)=-b,计算出参数a,b的值,然后求出f(1)及f'(1)的值,然后代入点斜式方程,即可得到曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求导数,利用导数的正负,可得函数g(x)的单调区间.
解答 解:(1)因为f(x)=x3+ax2+bx+1,所以f'(x)=3x2+2ax+b.…..(2分)
令x=1得f'(1)=3+2a+b.
由已知f'(1)=2a,所以3+2a+b=2a.解得b=-3.
又令x=2得f'(2)=12+4a+b.
由已知f'(2)=-b,所以12+4a+b=-b,解得a=-$\frac{3}{2}$.…..(4分)
所以f(x)=x3-$\frac{3}{2}$x2-3x+1,f(1)=-$\frac{5}{2}$.
又因为f′(1)=-3,….(6分)
故曲线y=f(x)在点(1,f(1))处的切线方程为y-(-$\frac{5}{2}$)=-3(x-1),即6x+2y-1=0.…..(8分)
(2)g(x)=f′(x)ex=(3x2-3x-3)ex,∴g′(x)=3(x-1)(x+2)ex,
由g′(x)>0,可得x<-2或x>1,函数的单调递增区间是(-∞,-2),(1,+∞)
由g′(x)<0,可得-2<x<1,函数的单调递减区间是(-2,1).
点评 本题主要考查了利用导数研究曲线上某点切线方程,函数的单调区间,以及方程组的求解等有关问题,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
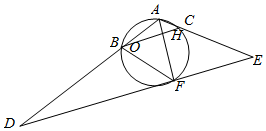 如图,在△ABC中,AH平分∠BAC,交△ABC的外接圆O于点F,过点F作DE∥BC.分别交AB,AC的延长线于D,E两点.
如图,在△ABC中,AH平分∠BAC,交△ABC的外接圆O于点F,过点F作DE∥BC.分别交AB,AC的延长线于D,E两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com