
分析 (1)根据函数奇偶性的定义建立方程即可求出a,根据分式函数的意义即可求出函数的定义域.
(2)利用函数单调性的定义,设出变量,利用作差法进行证明即可.
(3)根据函数奇偶性和单调性的性质将不等式进行转化求解即可.
解答 解:(1)要使函数有意义,则2x-1≠0,即2x≠1,即x≠0,
则函数的定义域为{x|x≠0},
∵函数f(x)=$\frac{1}{{{2^x}-1}}$+a是奇函数,可得f(x)+f(-x)=0,
∴$\frac{1}{{{2^x}-1}}$+a+$\frac{1}{{{2^{-x}}-1}}$+a=0,解得a=$\frac{1}{2}$,
∴函数f(x)=$\frac{1}{{{2^x}-1}}$+$\frac{1}{2}$,
(2)由(1)得f(x)=$\frac{1}{{{2^x}-1}}$+$\frac{1}{2}$,
则f(x)在(0,+∞)上都是减函数,证明如下
任取x1<x2则
f(x1)-f(x2)=$\frac{1}{{2}^{{x}_{1}}-1}-\frac{1}{{2}^{{x}_{2}}-1}$=$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{({2}^{{x}_{1}}-1)({2}^{{x}_{2}}-1)}$
当x1,x2∈(0,+∞)时,${2}^{{x}_{1}}-1$>0,${2}^{{x}_{2}}-1$>0,${2}^{{x}_{2}}-{2}^{{x}_{1}}>0$,
所以$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{({2}^{{x}_{1}}-1)({2}^{{x}_{2}}-1)}$>0,
有f(x1)-f(x2)>0
即f(x1)>f(x2),
则f(x)=$\frac{1}{{{2^x}-1}}$+$\frac{1}{2}$在(0,+∞)上是减函数;
(3)∵函数f(x)是奇函数且在(0,+∞)上是减函数,
∴由f(-m2+2m-1)+f(m2+3)<0
得f(m2+3)<-f(-m2+2m-1)=f(m2-2m+1),
∵m2+3>0,m2-2m+1=(m-1)2≥0,
∴m2+3>m2-2m+1,且(m-1)2≠0
即2m>-2且m≠1,得m>-1且m≠1.
点评 本题考查了函数奇偶性的性质以及函数单调性的证明方法定义法,解题的关键是理解奇函数的定义及单调性的证明方法,本题的重点是单调性的证明,其中判断符号是难点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 12 | C. | 24 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{17}$ | B. | $\frac{15\sqrt{3}+8}{34}$ | C. | $\frac{15-8\sqrt{3}}{34}$ | D. | $\frac{15+8\sqrt{3}}{34}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
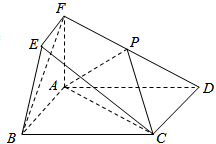 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=2,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=2,点P在棱DF上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com