
分析 根据同角的三角函数关系与三角恒等变换,利用诱导公式和弦化切公式,即可求出对应的各组数值.
解答 解:tanα=2,
(1)$\frac{2sin(α-π)3cos(-α)}{4sin(\frac{π}{2}+α)-9cos(α-\frac{3π}{2})}$=$\frac{2•(-sinα)•3cosα}{4cosα-9•(-sinα)}$=-6•$\frac{sinα}{4+9tanα}$=-$\frac{3}{11}$sinα;
又$\frac{sinα}{cosα}$=2,
∴cosα=$\frac{1}{2}$sinα,
∴sin2α+cos2α=sin2α+$\frac{1}{4}$sin2α=$\frac{5}{4}$sin2α=1,
∴sinα=±$\frac{2\sqrt{5}}{5}$,
∴原式=-$\frac{3}{11}$×(±$\frac{2\sqrt{5}}{5}$)=±$\frac{6\sqrt{5}}{55}$;
(2)4sin2α-3sinαcosα-5cos2α=$\frac{{4sin}^{2}α-3sinαcosα-{5cos}^{2}α}{{sin}^{2}α{+cos}^{2}α}$
=$\frac{{4tan}^{2}α-3tanα-5}{{tan}^{2}α+1}$
=$\frac{4{×2}^{2}-3×2-5}{{2}^{2}+1}$
=1;
(3)$\frac{1+sin2α}{1+sin2α+cos2α}$=$\frac{{sin}^{2}α{+cos}^{2}α+2sinαcosα}{2sinαcosα+{2cos}^{2}α}$
=$\frac{{(sinα+cosα)}^{2}}{2cosα(sinα+cosα)}$
=$\frac{sinα+cosα}{2cosα}$
=$\frac{1}{2}$tanα+$\frac{1}{2}$
=$\frac{1}{2}$×2+$\frac{1}{2}$
=$\frac{3}{2}$.
点评 本题考查了同角的三角函数关系与三角恒等变换,诱导公式和弦化切公式的应用问题,是基础题目.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{{e}^{2}-1}{2e-1}$,+∞) | B. | (-∞,$\frac{{e}^{2}-1}{2e-1}$) | C. | (0,$\frac{{e}^{2}-1}{2e-1}$) | D. | {$\frac{{e}^{2}-1}{2e-1}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
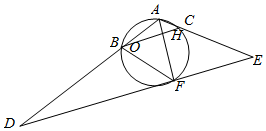 如图,在△ABC中,AH平分∠BAC,交△ABC的外接圆O于点F,过点F作DE∥BC.分别交AB,AC的延长线于D,E两点.
如图,在△ABC中,AH平分∠BAC,交△ABC的外接圆O于点F,过点F作DE∥BC.分别交AB,AC的延长线于D,E两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com