
 ln(2x+1)万美元,受美联储货币政策的影响,美元?值,由于生产加工签约和成品交付要经历一段时间,收益将因美元赔值而损失mx万美元,其中m为该时段美元的贬值指数是m∈(0,1),从而实际所得的加工费为f(x)=
ln(2x+1)万美元,受美联储货币政策的影响,美元?值,由于生产加工签约和成品交付要经历一段时间,收益将因美元赔值而损失mx万美元,其中m为该时段美元的贬值指数是m∈(0,1),从而实际所得的加工费为f(x)= ln(2x+1)-mx(万美元).
ln(2x+1)-mx(万美元).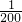 ,为确保企业实际所得加工费随X的增加而增加,该企业加工产品订单的金额X应在什么范围内?
,为确保企业实际所得加工费随X的增加而增加,该企业加工产品订单的金额X应在什么范围内? x万美元,己知该企业加工生产能力为x∈[10,20](其中X为产品订单的金额),试问美元的贬值指数m在何范围时,该企业加工生产将不会出现亏损.
x万美元,己知该企业加工生产能力为x∈[10,20](其中X为产品订单的金额),试问美元的贬值指数m在何范围时,该企业加工生产将不会出现亏损.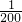 ,f(x)=
,f(x)= ln(2x+1)-
ln(2x+1)-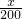 ,(其中x>0);
,(其中x>0);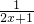 -
-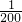 =
= ;
; ln(2x+1)-mx≥
ln(2x+1)-mx≥ x,即
x,即 +m≤
+m≤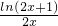 ,
,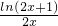 ,x∈[10,20],则
,x∈[10,20],则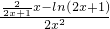 =
=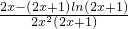 ;
;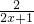 ]=-2ln(2x+1)<0,
]=-2ln(2x+1)<0,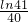 ,即m≤
,即m≤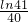 -
- ;
;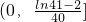 时,该企业加工生产不会亏损.
时,该企业加工生产不会亏损.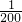 ,得f(x)=
,得f(x)= ln(2x+1)-
ln(2x+1)-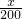 ,对f(x)求导,并令f′(x)>0,可解得x的值;即为所求.
,对f(x)求导,并令f′(x)>0,可解得x的值;即为所求. ln(2x+1)-mx≥
ln(2x+1)-mx≥ x恒成立,通过变形,得
x恒成立,通过变形,得 +m≤
+m≤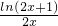 ,令g(x)=
,令g(x)=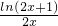 ,x∈[10,20],对g(x)求导,得g′(x)=
,x∈[10,20],对g(x)求导,得g′(x)=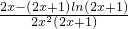 ;再令h(x)=2x-(2x+1)ln(2x+1),对h(x)求导,得h′(x)<0,从而得h(x)在[10,20]上单调递减,即h(20)≤h(x)≤h(10)<0,所以x∈[10,20]时,g(x)单调递减,从而得gmin(x)=g(20),即m≤g(20)-
;再令h(x)=2x-(2x+1)ln(2x+1),对h(x)求导,得h′(x)<0,从而得h(x)在[10,20]上单调递减,即h(20)≤h(x)≤h(10)<0,所以x∈[10,20]时,g(x)单调递减,从而得gmin(x)=g(20),即m≤g(20)- ;即得美元的贬值指数m的范围.
;即得美元的贬值指数m的范围.

科目:高中数学 来源: 题型:单选题
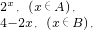 x0∈A,且f[f(x0)]∈A,则x0的取值范围是
x0∈A,且f[f(x0)]∈A,则x0的取值范围是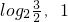 )
)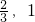 )
) ]
]查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高校 | 相关人数 | 抽取人数 |
| A | X | 1 |
| B | 36 | y |
| C | 54 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 的双曲线C2以A,B为焦点.若P是圆C1与双曲线C2的一个公共点,则|PA|+|PB|=
的双曲线C2以A,B为焦点.若P是圆C1与双曲线C2的一个公共点,则|PA|+|PB|=



查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
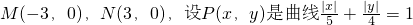 上的点,则下列式子恒成立的是
上的点,则下列式子恒成立的是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com