
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为![]() (θ为参数).
(θ为参数).
(1)当![]() 时,求直线l与曲线C的普通方程;
时,求直线l与曲线C的普通方程;
(2)若直线l与曲线C交于A,B两点,直线l倾斜角的范围为(0,![]() ],且P点的直角坐标为(0,2),求
],且P点的直角坐标为(0,2),求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(x+1)2+(y﹣1)2=1(2)
;(x+1)2+(y﹣1)2=1(2)![]()
【解析】
(1)将![]() 代入直线l的参数方程,消去参数t即可得到直线l的普通方程,由曲线C的参数方程消去参数θ即可得到曲线C的普通方程;
代入直线l的参数方程,消去参数t即可得到直线l的普通方程,由曲线C的参数方程消去参数θ即可得到曲线C的普通方程;
(2)利用参数的几何意义结合正弦型函数的图象及性质即可得解.
(1)∵![]() ,
,
∴直线l的参数方程为 ,消掉参数t,可得直线l的普通方程为
,消掉参数t,可得直线l的普通方程为![]() ,
,
∵C的参数方程为![]() (θ为参数)
(θ为参数)
∴可得(x+1)2+(y﹣1)2=1,即曲线C的普通方程为(x+1)2+(y﹣1)2=1.
(2)将l的参数方程为![]() (t为参数)代入圆的方程(x+1)2+(y﹣1)2=1得t2+2(sinα+cosα)t+1=0,
(t为参数)代入圆的方程(x+1)2+(y﹣1)2=1得t2+2(sinα+cosα)t+1=0,
设A,B所对应的参数分别为t1,t2,
则|PA||PB|=|t1t2|=1,|PA|+|PB|=|t1+t2|=2|sinα+cosα|,
所以 ,
,
当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别与
分别与![]() 交于异于极点的
交于异于极点的![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的虚轴的一个顶点为
的虚轴的一个顶点为![]() ,左顶点为
,左顶点为![]() ,双曲线
,双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的动点,当
上的动点,当![]() 取得最小值和最大值时,
取得最小值和最大值时,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,若
,若![]() ,则双曲线
,则双曲线![]() 的离心率为( ).
的离心率为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )
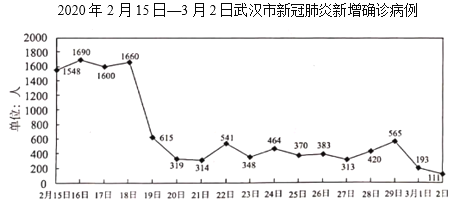
A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,有下列4个命题:
,有下列4个命题:
①若![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
②![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
③若![]() 为偶函数,且
为偶函数,且![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④若![]() 为奇函数,且
为奇函数,且![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
其中正确的命题为 .(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
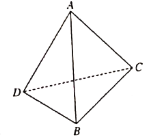
【题目】现有一副斜边长为10的直角三角板,将它们斜边![]() 重合,若将其中一个三角板沿斜边折起形成三棱锥
重合,若将其中一个三角板沿斜边折起形成三棱锥![]() ,如图所示,已知
,如图所示,已知![]() ,
,![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积为______;该三棱锥体积的最大值为_______.
的外接球的表面积为______;该三棱锥体积的最大值为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动直线与![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两不同点,且
两不同点,且![]() 的面积
的面积![]() ,其中
,其中![]() 为坐标原点
为坐标原点
(1)若动直线![]() 垂直于
垂直于![]() 轴.求直线
轴.求直线![]() 的方程;
的方程;
(2)证明:![]() 和
和![]() 均为定值;
均为定值;
(3)椭圆![]() 上是否存在点
上是否存在点![]() ,
,![]() ,
,![]() ,使得三角形面积
,使得三角形面积![]() 若存在,判断
若存在,判断![]() 的形状;若不存在,请说明理由
的形状;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,过焦点做倾斜角为的120°的直线交
,过焦点做倾斜角为的120°的直线交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,
为坐标原点,![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过抛物线焦点,且与坐标轴不垂直的直线l交抛物线于![]() ,
,![]() 两点,
两点,![]() ,
,![]() 在抛物线上,且
在抛物线上,且![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() 四点都在圆
四点都在圆![]() 上,求圆
上,求圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:![]() 是无穷数列,若存在正整数k使得对任意
是无穷数列,若存在正整数k使得对任意![]() ,均有
,均有![]() 则称
则称![]() 是近似递增(减)数列,其中k叫近似递增(减)数列
是近似递增(减)数列,其中k叫近似递增(减)数列![]() 的间隔数
的间隔数
(1)若![]() ,
,![]() 是不是近似递增数列,并说明理由
是不是近似递增数列,并说明理由
(2)已知数列![]() 的通项公式为
的通项公式为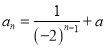 ,其前n项的和为
,其前n项的和为![]() ,若2是近似递增数列
,若2是近似递增数列![]() 的间隔数,求a的取值范围:
的间隔数,求a的取值范围:
(3)已知![]() ,证明
,证明![]() 是近似递减数列,并且4是它的最小间隔数.
是近似递减数列,并且4是它的最小间隔数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com