
【题目】已知双曲线![]() 的虚轴的一个顶点为
的虚轴的一个顶点为![]() ,左顶点为
,左顶点为![]() ,双曲线
,双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的动点,当
上的动点,当![]() 取得最小值和最大值时,
取得最小值和最大值时,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,若
,若![]() ,则双曲线
,则双曲线![]() 的离心率为( ).
的离心率为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】某中学有教师400人,其中高中教师240人.为了了解该校教师每天课外锻炼时间,现利用分层抽样的方法从该校教师中随机抽取了100名教师进行调查,统计其每天课外锻炼时间(所有教师每天课外锻炼时间均在![]() 分钟内),将统计数据按
分钟内),将统计数据按![]() ,
,![]() ,
,![]() ,…,
,…,![]() 分成6组,制成频率分布直方图如下:
分成6组,制成频率分布直方图如下:
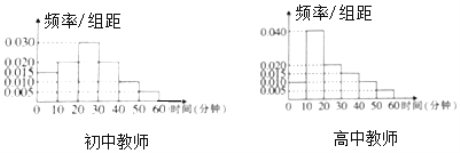
假设每位教师每天课外锻炼时间相互独立,并称每天锻炼时间小于20分钟为缺乏锻炼.
(1)试估计本校教师中缺乏锻炼的人数;
(2)若从参与调查,且每天课外锻炼时间在![]() 内的该校教师中任取2人,求至少有1名初中教师被选中的概率.
内的该校教师中任取2人,求至少有1名初中教师被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 与底面ABC所成的二面角为
与底面ABC所成的二面角为![]() ,E,F分别是棱
,E,F分别是棱![]() ,
,![]() 的中点.
的中点.

(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与底面ABC所成的角的大小.
与底面ABC所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学一班级1999级同学举行20周年聚会,该班共来了12位同学,其中女同学6位,聚会过程中有一个游戏环节,在游戏环节中,需要随机从中选出2位同学代表,进行男女搭配完成该项游戏,因此,每次选出的2位同学是一男一女,才算“有效选择”;否则视为“无效选择”,继续下一次选择,直到成为“有效选择”为止.
(1)求第一次随机选出的2位同学是“有效选择”的概率;
(2)设第一次选出的2位同学代表中女同学人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某晚会上某歌舞节目的表演者是3个女孩和4个男孩.演出结束后,7个人合影留念(3个人站在前排,4个人站在后排),其中男孩甲、乙要求站在一起,女孩丙不能站在两边,不同站法的种数为( )
A.96B.240C.288D.432
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别是椭圆
分别是椭圆![]()
![]()
![]() 的左右焦点,其焦距为
的左右焦点,其焦距为![]() ,过
,过![]() 的直线与
的直线与![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的周长是
的周长是![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() 是
是![]() 上的动点,从点
上的动点,从点![]() (
(![]() 是坐标系原点)向圆
是坐标系原点)向圆![]() 作两条切线,分别交
作两条切线,分别交![]() 于
于![]() ,
,![]() 两点.已知直线
两点.已知直线![]() ,
,![]() 的斜率存在,并分别记为
的斜率存在,并分别记为![]() ,
,![]() .
.
(ⅰ)求证:![]() 为定值;
为定值;
(ⅱ)试问![]() 是否为定值?若是,求出该值;若不是,请说明理由.
是否为定值?若是,求出该值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为![]() (θ为参数).
(θ为参数).
(1)当![]() 时,求直线l与曲线C的普通方程;
时,求直线l与曲线C的普通方程;
(2)若直线l与曲线C交于A,B两点,直线l倾斜角的范围为(0,![]() ],且P点的直角坐标为(0,2),求
],且P点的直角坐标为(0,2),求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】发展“会员”、提供优惠,成为不少实体店在网购冲击下吸引客流的重要方式.某连锁店为了吸引会员,在2019年春节期间推出一系列优惠促销活动.抽奖返现便是针对“白金卡会员”、“金卡会员”、“银卡会员”、“基本会员”不同级别的会员享受不同的优惠的一项活动:“白金卡会员”、“金卡会员”、“银卡会员”、“基本会员”分别有4次、3次、2次、1次抽奖机会.抽奖机如图:抽奖者第一次按下抽奖键,在正四面体的顶点![]() 出现一个小球,再次按下抽奖键,小球以相等的可能移向邻近的顶点之一,再次按下抽奖键,小球又以相等的可能移向邻近的顶点之一……每一个顶点上均有一个发光器,小球在某点时,该点等可能发红光或蓝光,若出现红光则获得2个单位现金,若出现蓝光则获得3个单位现金.
出现一个小球,再次按下抽奖键,小球以相等的可能移向邻近的顶点之一,再次按下抽奖键,小球又以相等的可能移向邻近的顶点之一……每一个顶点上均有一个发光器,小球在某点时,该点等可能发红光或蓝光,若出现红光则获得2个单位现金,若出现蓝光则获得3个单位现金.
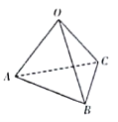
(1)求“银卡会员”获得奖金的分布列;
(2)![]() 表示第
表示第![]() 次按下抽奖键,小球出现在
次按下抽奖键,小球出现在![]() 点处的概率.
点处的概率.
①求![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
②写出![]() 与
与![]() 关系式,并说明理由.
关系式,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com