练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

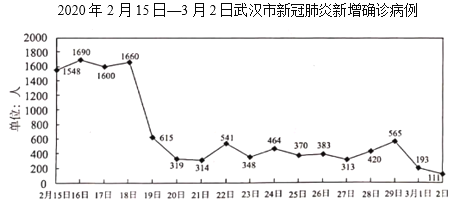
    【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图．则下列说法不正确的是（ ）

    A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数

    B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果，但防控要求不能降低

    C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天

    D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人

    【答案】D

    【解析】

    根据图表中提供的信息，对应各选项即可判断其真假．

    对于A，由图可知，2020年2月19日，武汉市新增新冠肺炎确诊病例从2月18日的1660人大幅下降至615人，所以A正确；

    对于B，从2020年2月19日起至2月29日，武汉市新增新冠肺炎确诊病例大约在300-615之间，3月起继续减少，没有出现大幅增加，所以B正确；

    对于C，由图可知，2020年2月19日至3月2日，武汉市新增新冠肺炎确诊病例低于400人的有，2月20日，21日，23日，25日，26日，27日，3月1日，2日，共8天，所以C正确；

    对于D，2020年2月15日到3月2日中，武汉市新增新冠肺炎确诊病例最多的是2月16日1690例，最少的是3月2日111例，1690-111=1579，所以D不正确．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】请从下面三个条件中任选一个，补充在下面的横线上，并作答．

    ①AB⊥BC，②FC与平面ABCD所成的角为，③∠ABC．

    如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，PA⊥平面ABCD，且PA＝AB＝2，，PD的中点为F．

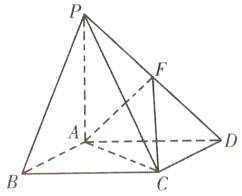
    （1）在线段AB上是否存在一点G，使得AF平面PCG？若存在，指出G在AB上的位置并给以证明；若不存在，请说明理由；

    （2）若_______，求二面角F﹣AC﹣D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某小学一班级1999级同学举行20周年聚会，该班共来了12位同学，其中女同学6位，聚会过程中有一个游戏环节，在游戏环节中，需要随机从中选出2位同学代表，进行男女搭配完成该项游戏，因此，每次选出的2位同学是一男一女，才算“有效选择”；否则视为“无效选择”，继续下一次选择，直到成为“有效选择”为止.

    （1）求第一次随机选出的2位同学是“有效选择”的概率；

    （2）设第一次选出的2位同学代表中女同学人数为，求随机变量的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过抛物线的焦点F任作两条互相垂直的直线，，分别与抛物线E交于A，B两点和C，D两点，则的最小值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，分别是椭圆的左右焦点，其焦距为，过的直线与交于，两点，且的周长是.

    （1）求的方程；

    （2）若是上的动点，从点(是坐标系原点)向圆作两条切线，分别交于，两点.已知直线，的斜率存在，并分别记为，.

    （ⅰ）求证：为定值；

    （ⅱ）试问是否为定值？若是，求出该值；若不是，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）判断函数在点处的切线是否过定点？若过，求出该点的坐标；若不过，请说明理由．

    （2）若有最大值，证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，直线l的参数方程为（t为参数），曲线C的参数方程为（θ为参数）.

    （1）当时，求直线l与曲线C的普通方程；

    （2）若直线l与曲线C交于A，B两点，直线l倾斜角的范围为（0，]，且P点的直角坐标为（0，2），求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的右焦点为F，直线l与C交于M，N两点.

    （1）若l过点F，点M，N到直线y＝2的距离分别为d1，d2，且，求l的方程；

    （2）若点M的坐标为（0，1），直线m过点M交C于另一点N′，当直线l与m的斜率之和为2时，证明：直线NN′过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图．则下列说法不正确的是（ ）

    A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数

    B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果，但防控要求不能降低

    C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天

    D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人

    查看答案和解析>>

    同步练习册答案