
分析 可作图:设A(1,1),从而$\overrightarrow{OA}=\overrightarrow{a}$,可作$\overrightarrow{OB}=\overrightarrow{b}$,从而$\overrightarrow{AB}=\overrightarrow{b}-\overrightarrow{a}$,根据条件便可得到$∠B=\frac{π}{4},OA=\sqrt{2}$,这样在△AOB中,由正弦定理即可得出AB=2sin∠AOB,从而可以得出AB的最大值,即得出$|\overrightarrow{b}-\overrightarrow{a}|$的最大值.
解答 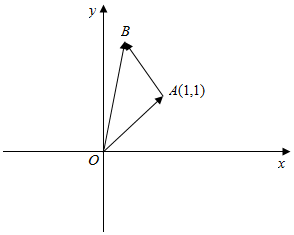 解:如图,设A(1,1),连接OA,则$\overrightarrow{OA}=\overrightarrow{a}$,作$\overrightarrow{OB}=\overrightarrow{b}$,则$\overrightarrow{AB}=\overrightarrow{b}-\overrightarrow{a}$;
解:如图,设A(1,1),连接OA,则$\overrightarrow{OA}=\overrightarrow{a}$,作$\overrightarrow{OB}=\overrightarrow{b}$,则$\overrightarrow{AB}=\overrightarrow{b}-\overrightarrow{a}$;
∵$\overrightarrow{b}$与$\overrightarrow{b}-\overrightarrow{a}$的夹角为$\frac{π}{4}$;
∴$∠B=\frac{π}{4}$,且OA=$\sqrt{2}$;
∴在△AOB中,由正弦定理得,$\frac{AB}{sin∠AOB}=\frac{OA}{sinB}$;
∴$AB=\frac{\sqrt{2}}{sin\frac{π}{4}}•sin∠AOB=2sin∠AOB≤2$,当且仅当$∠AOB=\frac{π}{2}$时取“=”;
∴AB的最大值为2,即$|\overrightarrow{b}-\overrightarrow{a}|$的最大值为2.
故答案为:2.
点评 考查根据点的坐标求向量的坐标,两点间的距离公式,向量夹角的概念,以及正弦定理,正弦函数的值域.


科目:高中数学 来源: 题型:选择题
| A. | [-2,1) | B. | (1,+∞) | C. | (1,2] | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
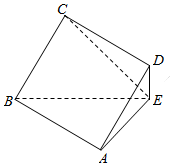 如图,四边形ABCD是正方形,DE⊥平面ABE,BE=3DE,DE=3,AB⊥AE.
如图,四边形ABCD是正方形,DE⊥平面ABE,BE=3DE,DE=3,AB⊥AE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com