
分析 (1)根据题意写出sinα与cosα的值,再得出β=α-60°,利用两角差的正弦值公式求出sinβ;
(2)根据α、β的取值范围得出α-$\frac{π}{4}$与$\frac{3π}{4}$+β的取值范围,利用同角的三角函数关系和三角恒等变换,即可求出sin(α+β)的值.
解答 解:(1)根据题意,sinα=$\frac{12}{13}$,cosα=-$\frac{5}{13}$,
将点A沿单位圆按顺时针方向旋转60°,到达点B,β=α-60°,
sinβ=sin(α-60°)=sinαcos60°-cosαsin60°=$\frac{12}{13}$×$\frac{1}{2}$-(-$\frac{5}{13}$)×$\frac{\sqrt{3}}{2}$=$\frac{12+5\sqrt{3}}{26}$;
(2)∵α∈($\frac{π}{4}$,$\frac{3π}{4}$),∴α-$\frac{π}{4}$∈(0,$\frac{π}{2}$),
β∈(0,$\frac{π}{4}$),∴$\frac{3π}{4}$+β∈($\frac{3π}{4}$,π);
又∵cos($α-\frac{π}{4}$)=$\frac{3}{5}$,∴sin(α-$\frac{π}{4}$)=$\frac{4}{5}$,
∵sin($\frac{3π}{4}$+β)=$\frac{5}{13}$,∴cos($\frac{3π}{4}$+β)=-$\frac{12}{13}$;
∴sin(α+β)=-cos[$\frac{π}{2}$+(α+β)]
=-cos[(α-$\frac{π}{4}$)+($\frac{3π}{4}$+β)]
=-cos(α-$\frac{π}{4}$)cos($\frac{3π}{4}$+β)+sin(α-$\frac{π}{4}$)sin($\frac{3π}{4}$+β)
=-$\frac{3}{5}$×(-$\frac{12}{13}$)+$\frac{4}{5}$×$\frac{5}{13}$
=$\frac{56}{65}$.
点评 本题考查了三角函数的定义与同角的三角函数关系、三角恒等变换公式的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
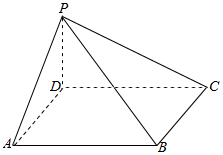 如图所示,四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠DAB=60°,PA=PB=PD=a.
如图所示,四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠DAB=60°,PA=PB=PD=a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com