练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．课外兴趣小组共有15人，其中9名男生，6名女生，其中1名为组长，现要选3人参加数学竞赛，分别求出满足下列各条件的不同选法数．
    （1）要求组长必须参加；
    （2）要求选出的3人中至少有1名女生；
    （3）要求选出的3人中至少有1名女生和1名男生．

    分析 （1）组长必须参加，再从其它14个人中再选2人即可问题得以解决，
    （2）选出的3人中至少有1名女生，分三类，1名女生2名男生，2名女生1名男生，3名女生，根据分类计数原理可得，
    （3）选出的3人中至少有1名女生和1名男生，1名女生2名男生，2名女生1名男生，根据分类计数原理可得．

    解答 解：（1）组长必须参加，再从其它14个人中再选2人即可，共有的选法种数为C142=91种，
    （2）选出的3人中至少有1名女生，C61C92+C62C91+C63=371种，
    （3）选出的3人中至少有1名女生和1名男生，C61C92+C62C91=351种，

    点评 本题考查了分类计数原理，关键是分类，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

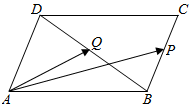    7．在边长为2的菱形ABCD中，∠BAD=60°，P，Q分别是BC，BD的中点，则向量$\overrightarrow{AP}$与$\overrightarrow{AQ}$的夹角的余弦值为$\frac{3\sqrt{21}}{14}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．盒子中共有12盒奶，工商人员从中任取3盒进行质量检查，则不同抽取方法的种数是（　　）
    A．22B．48C．84D．220

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．在数列{an}中，a1=1，an=an-1+3n-1（n≥2），则数列{an}的通项公式为$\frac{{3}^{n}-1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知A={a+2，（a+1）2，a2+3a+3}，且1∈A，求实数2013a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．下列程序运行的结果是5050．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．在（x-$\frac{3}{x}$+2）5的展开式中，x3的系数为25．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知点F1，F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左，右焦点，过F2且垂直于x轴的直线与双曲线交于M，N两点，若$\overrightarrow{M{F}_{1}}$•$\overrightarrow{N{F}_{1}}$＞0，则该双曲线的离心率e的取值范围是（　　）
    A．（$\sqrt{2}$，$\sqrt{2}$+1）B．（1，$\sqrt{2}$+1）C．（1，$\sqrt{3}$）D．$（{\sqrt{3}，+∞}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知Sn是等比数列{an}的前n项和，若$\frac{{S}_{m}}{{S}_{2m}}$=$\frac{1}{5}$（m∈N*），则$\frac{{a}_{m}}{{a}_{2m}}$=（　　）
    A．$\frac{1}{4}$B．4C．$\frac{1}{5}$D．5

    查看答案和解析>>

    同步练习册答案