
下表是某市从3月份中随机抽取的10天空气质量指数(AQI)和“PM2.5”(直径小于等于2.5微米的颗粒物)24小时平均浓度的数据,空气质量指数(AQI)小于100表示空气质量优良.
| 日期编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 空气质量指数(AQI) | 179 | 40 | 98 | 124 | 29 | 133 | 241 | 424 | 95 | 89 |
| “PM2.5”24小时平均浓度( | 135 | 5 | 80 | 94 | 80 | 100 | 190 | 387 | 70 | 66 |
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件M为“抽取的两个日期中,当天‘PM2.5’的24小时平均浓度不超过75 ”,求事件M发生的概率;
”,求事件M发生的概率;
(3)在上表数据中,在表示空气质量优良的日期中,随机抽取3天,记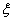 为“PM2.5”24小时平均浓度不超过75
为“PM2.5”24小时平均浓度不超过75 的天数,求
的天数,求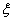 的分布列和数学期望.
的分布列和数学期望.
 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
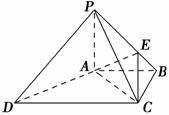
如图,在四棱锥P ABCD中,PA⊥底面ABCD,PC⊥AD,底面ABCD为梯形,AB∥DC,AB⊥BC,PA=AB=BC,点E在棱PB上,且PE=2EB.
(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,动点P在正方体ABCD — A1B1C1D1的对角线BD1上, 过点P作垂直于平面BB1D1D的直线,与正方体表面相交于M,Ⅳ, 设BP=x,MN =y,则函数y=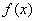 的图象大致是( )
的图象大致是( )
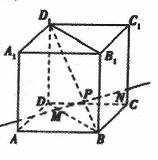
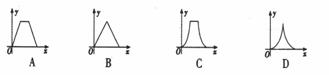
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com