已知函数
.
(I)若函数
为奇函数，求实数
的值；
(II)若对任意的
，都有
成立，求实数的取值范围．
应用题作业本系列答案科目：高中数学 来源： 题型：解答题
在圆
上任取一点
，设点在
轴上的正投影为点
．当点在圆上运动时，动点
满足
，动点形成的轨迹为曲线
.
（1）求曲线的方程；
（2）已知点
，若
、
是曲线上的两个动点，且满足
，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
．
（1）请在所给的平面直角坐标系中画出函数
的图像；
（2）根据函数的图像回答下列问题：
①求函数的单调区间；
②求函数的值域；
③求关于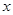
的方程
在区间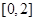
上解的个数．
（回答上述3个小题都只需直接写出结果，不需给出演算步骤）
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某创业投资公司拟投资开发某种新能源产品，估计能获得10万元到1000万元的投资收益．现准备制定一个对科研课题组的奖励方案：奖金
（单位：万元）随投资收益
（单位：万元）的增加而增加，且奖金不超过9万元，同时奖金不超过投资收益的20%．
（1）若建立函数
模型制定奖励方案，试用数学语言表述该公司对奖励函数
模型的基本要求，并分析函数
是否符合这个要求，并说明原因；
（2）若该公司采用函数
作为奖励函数模型，试确定最小的正整数
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数
，恒过定点
．
（1）求实数
；
（2）在（1）的条件下，将函数
的图象向下平移1个单位，再向左平移个单位后得到函数
，设函数的反函数为
，直接写出的解析式；
（3）对于定义在
上的函数
，若在其定义域内，不等式
恒成立，求实数
的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
. （Ⅱ）
.
，得到恒等式
对一切
恒成立，不难得到
对
恒成立，从而只需
,
在
上的最小值，利用函数的单调性易得
.
所以
，均有
即
成立，
，
的图象；
在区间
上有最大值
，求实数
的值
（
）在
上的最大值为23，求a的值.
.
恒成立，求
的最大值；
为常数，且
，记
，求
的最小值.