
分析 (1)利用函数单调性的定义进行证明:在区间[-1,1]任取x1、x2,且x1<x2,利用函数为奇函数的性质结合已知条件中的分式,可以证得f(x1)-f(x2)<0,所以函数f(x)是[-1,1]上的增函数.
(2)根据函数的单调性得到关于x的不等式组,解得即可,
(3)根据函数f(x)≤m2-2am+1对所有的x∈[-1,1],a∈[-1,1]恒成立,说明f(x)的最大值1小于或等于右边,因此先将右边看作a的函数,m为参数系数,解不等式组,即可得出m的取值范围.
解答 解:(1)任取x1、x2∈[-1,1],且x1<x2,f(x)是奇函数
则f(x1)-f(x2)=f(x1)+f(-x2)=$\frac{f({x}_{1})+f({x}_{2})}{{x}_{1}+(-{x}_{2})}$(x1-x2)
∵$\frac{f(a)+f(b)}{a+b}$>0,即$\frac{f({x}_{1})+f({x}_{2})}{{x}_{1}+(-{x}_{2})}$>0,
∵x1+(-x2)<0,
∴f(x1)-f(x2)<0.
则f(x)是[-1,1]上的增函数.
(2)f(x)是[-1,1]上的增函数,
∴$\left\{\begin{array}{l}{x+\frac{1}{2}<2x-1}\\{-1<x+\frac{1}{2}≤1}\\{-1≤2x-1<1}\end{array}\right.$,
解得0≤x≤$\frac{1}{2}$,
故不等式的解集为[0,$\frac{1}{2}$],
(3)∵f(x)是[-1,1]上的增函数,
∴f(x)max=f(1)=1,
∴m2-2am+1≥1对所有的x∈[-1,1],a∈[-1,1]恒成立,
即m2-2am≥0恒成立,
当m=0时,0≥0成立,
当m≠0时,令g(a)=-2ma+m2,g(a)是关于a∈[-1,1]的一次函数,
只须$\left\{\begin{array}{l}{g(1)=-2m+{m}^{2}≥0}\\{g(-1)=2m+{m}^{2}≥0}\end{array}\right.$,
解得m≤-2或m≥2或m=0
综上所述m=0,或m≤-2或m≥2
点评 本题考查了抽象函数的单调性与函数的值域、不等式恒成立等知识点,属于中档题,解题时应该注意题中的主元与次元的处理.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{2},-2})$ | B. | (-1,-2) | C. | $({2,\frac{1}{4}})$ | D. | $({-\frac{1}{2},-4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
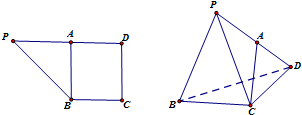 如图,矩形ABCD和直角三角形ABP有共同的边AB,且PA=AD=3,DC=4,沿BD把平面DBP折起,使AC=$\sqrt{7}$.
如图,矩形ABCD和直角三角形ABP有共同的边AB,且PA=AD=3,DC=4,沿BD把平面DBP折起,使AC=$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
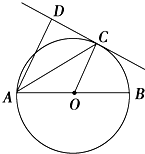 如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 任何一个算法一定含有顺序结构 | |
| B. | 一个算法可能同时含有顺序结构、条件结构、循环结构 | |
| C. | 循环结构中一定包含条件结构 | |
| D. | 条件结构中一定包含循环结构 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com