
| A. | 18 | B. | 22 | C. | 12 | D. | 24 |
分析 由直线l:y=$\sqrt{3}$x+2与圆O:x2+y2=4组成方程组,求出点A、B的坐标;
再求出过点A、B的圆O的切线,由此求出点C的坐标,得出$\overrightarrow{OC}$;
求出将向量$\overrightarrow{OC}$绕原点O逆时针旋转角度θ后,得到向量$\overrightarrow{OD}$,
计算$\overrightarrow{AD}$•$\overrightarrow{BD}$的最大值即可.
解答 解:由直线l:y=$\sqrt{3}$x+2与圆O:x2+y2=4组成方程组,
即$\left\{\begin{array}{l}{y=\sqrt{3}x+2}\\{{x}^{2}{+y}^{2}=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\sqrt{3}}\\{y=-1}\end{array}\right.$;
∴点A(0,2),B(-$\sqrt{3}$,-1);
过点A、B作圆O的切线分别为y=2,和y+1=-$\sqrt{3}$(x+$\sqrt{3}$),
由$\left\{\begin{array}{l}{y=2}\\{y+1=-\sqrt{3}(x+\sqrt{3})}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-2\sqrt{3}}\\{y=2}\end{array}\right.$;
∴C(-2$\sqrt{3}$,2),
∴$\overrightarrow{OC}$=(-2$\sqrt{3}$,2);
即$\overrightarrow{OC}$=(4cos$\frac{5π}{6}$,4sin$\frac{5π}{6}$);
将向量$\overrightarrow{OC}$绕原点O逆时针旋转角度θ后,得到向量$\overrightarrow{OD}$,
∴$\overrightarrow{OD}$=(4cos($\frac{5π}{6}$+θ),4sin($\frac{5π}{6}$+θ)),
∴$\overrightarrow{AD}$•$\overrightarrow{BD}$=4cos($\frac{5π}{6}$+θ)•(4cos($\frac{5π}{6}$+θ)+$\sqrt{3}$)+(4sin($\frac{5π}{6}$+θ)-2)•(4sin($\frac{5π}{6}$+θ)+1)
=4$\sqrt{3}$cos($\frac{5π}{6}$+θ)-4sin($\frac{5π}{6}$+θ)+14
=8cos($\frac{5π}{6}$+θ+$\frac{π}{6}$)+14;
当θ=π时,$\overrightarrow{AD}$•$\overrightarrow{BD}$取得最大值是8+14=22.
故选:B.
点评 本题考查了直线与圆的应用问题,也考查了平面向量的数量积运算和三角函数的应用问题,是综合性题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
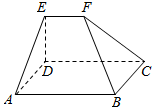 如图所示的几何体中,底面ABCD是矩形,AB=9,BC=6,EF∥平面ABCD,EF=3,△ADE和△BCF都是正三角形,求几何体EFABCD的体积.
如图所示的几何体中,底面ABCD是矩形,AB=9,BC=6,EF∥平面ABCD,EF=3,△ADE和△BCF都是正三角形,求几何体EFABCD的体积.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1 | B. | 0.16 | C. | 0.2 | D. | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com