
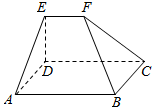
 如图所示的几何体中,底面ABCD是矩形,AB=9,BC=6,EF∥平面ABCD,EF=3,△ADE和△BCF都是正三角形,求几何体EFABCD的体积.
如图所示的几何体中,底面ABCD是矩形,AB=9,BC=6,EF∥平面ABCD,EF=3,△ADE和△BCF都是正三角形,求几何体EFABCD的体积. 分析 过F,E做与平面ABCD垂直的平面,这个平面把几何体分割成三部分,包括一个三棱柱和两个四棱锥,其中两个四棱锥的体积相等,三者相加得到结果.
解答 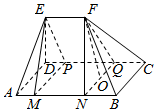 解分别过E,F作平面EMP⊥平面ABCD,平面FNQ⊥平面ABCD,交线分别为MP,NQ.
解分别过E,F作平面EMP⊥平面ABCD,平面FNQ⊥平面ABCD,交线分别为MP,NQ.
∵△ADE和△BCF都是正三角形,AD=BC,∴AE=BF.
∵EF∥平面ABCD,∴EF∥AB∥CD.
∴四边形ABFE,CDEF是等腰梯形.
∴CQ=NB=DP=AM=$\frac{1}{2}$(AB-EF)=3,FN=FQ=$\sqrt{F{B}^{2}-N{B}^{2}}$=3$\sqrt{3}$.
过F作FO⊥NQ于O,则FO⊥平面ABCD.且O为NQ的中点.
∴FO=$\sqrt{F{N}^{2}-N{O}^{2}}$=3$\sqrt{2}$.
∴VE-ADPM=VF-BCQN=$\frac{1}{3}{S}_{矩形BCQN}•FO$=$\frac{1}{3}×3×6×3\sqrt{2}$=18$\sqrt{2}$.
VEMP-FNQ=S△FNQ•EF=$\frac{1}{2}×6×3\sqrt{2}×3$=27$\sqrt{2}$.
∴几何体EFABCD的体积V=VEMP-FNQ+VE-ADPM+VF-BCQN=63$\sqrt{2}$.
点评 题考查不规则几何体的体积求法,通常将几何体分解成规则几何体计算体积.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | n=2011时,该命题成立 | B. | n=2013时,该命题成立 | ||
| C. | n=2011时,该命题不成立 | D. | n=2013时,该命题不成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,设计一个正四棱锥形冷水塔,高是3米,底面的边长是8米:
如图,设计一个正四棱锥形冷水塔,高是3米,底面的边长是8米:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 22 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com