
 如图,设计一个正四棱锥形冷水塔,高是3米,底面的边长是8米:
如图,设计一个正四棱锥形冷水塔,高是3米,底面的边长是8米:分析 (1)求出正四棱锥形的体积即可;
(2)求出斜高,在计算侧面积.
解答 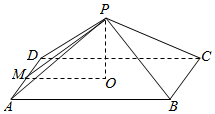 解:(1)V=$\frac{1}{3}$S正方形ABCD•h=$\frac{1}{3}×{8}^{2}×3$=64.
解:(1)V=$\frac{1}{3}$S正方形ABCD•h=$\frac{1}{3}×{8}^{2}×3$=64.
∴正四棱锥形冷水塔的容积为64立方米.
(2)取底面ABCD的中心O,AD的中点M,连结PO,OM,PM.
则PO⊥平面ABCD,PM⊥AD,
∴PO=h=3,OM=$\frac{1}{2}AB=4$,
∴PM=$\sqrt{P{O}^{2}+O{M}^{2}}$=5,
∴S△PAD=$\frac{1}{2}AD•PM$=$\frac{1}{2}×8×5$=20.
∴S侧面积=4S△PAD=80.
∴制造这个冷水塔的侧面需要80平方米的钢板.
点评 本题考查了棱锥的体积与侧面积计算,属于基础题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
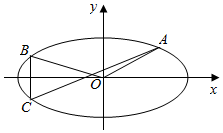 如图,已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且经过过点P(2,1).
如图,已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且经过过点P(2,1).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
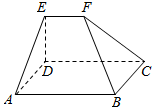 如图所示的几何体中,底面ABCD是矩形,AB=9,BC=6,EF∥平面ABCD,EF=3,△ADE和△BCF都是正三角形,求几何体EFABCD的体积.
如图所示的几何体中,底面ABCD是矩形,AB=9,BC=6,EF∥平面ABCD,EF=3,△ADE和△BCF都是正三角形,求几何体EFABCD的体积.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com