
已知二次函数f(x)的二次项系数为a,且不等式f(x)>2x的解集为(-1,3).
(1)若函数g(x)=xf(x)在区间 内单调递减,求a的取值范围;
内单调递减,求a的取值范围;
(2)当a=-1时,证明方程f(x)=2x3-1仅有一个实数根;
(3)当x∈[0,1]时,试讨论|f(x)+(2a-1)x+3a+1|≤3成立的充要条件.
(1)(-∞,-1](2)见解析(3)-5≤a<0
【解析】(1)∵f(x)-2x>0的解集为(-1,3),
∴可设f(x)-2x=a(x+1)(x-3),且a<0,
因而f(x)=a(x+1)(x-3)+2x=ax2+2(1-a)x-3a①
g(x)=xf(x)=ax3+2(1-a)x2-3ax,
∵g(x)在区间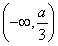 内单调递减,
内单调递减,
∴g′(x)=3ax2+4(1-a)x-3a在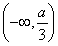 上的函数值非正,
上的函数值非正,
由于a<0,对称轴x=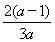 >0,故只需g′
>0,故只需g′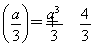 a(1-a)-3a≤0,注意到a<0,∴a2+4(1-a)-9≥0,得a≤-1或a≥5(舍去).
a(1-a)-3a≤0,注意到a<0,∴a2+4(1-a)-9≥0,得a≤-1或a≥5(舍去).
故所求a的取值范围是(-∞,-1].
(2)a=-1时,方程f(x)=2x3-1仅有一个实数根,即证方程2x3+x2-4x-4=0仅有一个实数根.令h(x)=2x3+x2-4x-4,由h′(x)=6x2+2x-4=0,得x1=-1,x2=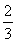 ,易知h(x)在(-∞,-1),
,易知h(x)在(-∞,-1),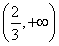 上递增,在
上递增,在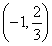 上递减,h(x)的极大值h(-1)=-1<0,故函数h(x)的图象与x轴仅有一个交点,∴a=-1时,方程f(x)=2x3-1仅有一个实数根,得证.
上递减,h(x)的极大值h(-1)=-1<0,故函数h(x)的图象与x轴仅有一个交点,∴a=-1时,方程f(x)=2x3-1仅有一个实数根,得证.
(3)设r(x)=f(x)+(2a-1)x+3a+1=ax2+x+1,r(0)=1,对称轴为x=-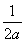 ,
,
由题意,得 或
或
解出-5≤a<0,
故使|f(x)+(2a-1)x+3a+1|≤3成立的充要条件是-5≤a<0


科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测5练习卷(解析版) 题型:填空题
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测3练习卷(解析版) 题型:填空题
若-9,a,-1成等差数列,-9,m,b,n,-1成等比数列,则ab=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测2练习卷(解析版) 题型:填空题
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB= BD,BC=2BD,则sin C的值为________.
BD,BC=2BD,则sin C的值为________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测1练习卷(解析版) 题型:填空题
若a>1,设函数f(x)=ax+x-4的零点为m,函数g(x)=logax+x-4的零点为n,则 +
+ 的最小值为________.
的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用阶段检测1练习卷(解析版) 题型:填空题
若函数f(x)=ln x- ax2-2x(a≠0)存在单调递减区间,则实数a的取值范围是______.
ax2-2x(a≠0)存在单调递减区间,则实数a的取值范围是______.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用8练习卷(解析版) 题型:解答题
如图所示,A,B分别是单位圆与x轴、y轴正半轴的交点,点P在单位圆上,∠AOP=θ(0<θ<π),C点坐标为(-2,0),平行四边形OAQP的面积为S.

(1)求 ·
· +S的最大值;
+S的最大值;
(2)若CB∥OP,求sin  的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用5练习卷(解析版) 题型:填空题
下面四个图象中,有一个是函数f(x)= x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于________.
x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)图象,则f(-1)等于________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com