考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)求出函数的定义域,求出导函数,令导函数大于0,求出x的范围,通过讨论x的范围与定义域的关系,求出递增区间和递减区间
(Ⅱ)通过构造函数g(x),利用导函数研究g(x)的单调性,利用函数的单调性,求出函数的最小值,即得整数k的最大值.
解答:
解:(Ⅰ)由
f(x)=知x∈(-1,0)∪(0,+∞).
∴
f′(x)=-,令h(x)=1+(x+1)ln(x+1)
则h′(x)=1+ln(x+1),令h′(x)=0,得
x=-1易得h(x)在
(-1,-1)上递减,在
(-1,+∞)上递增.
∴
h(x)min=h(-1)=1->0,∴f′(x)<0
故f(x)的单调减区间为(-1,0),(0,+∞).
(Ⅱ)当x>0时,
f(x)>恒成立,即
k<对x>0恒成立.
令
g(x)=(x>0),需k<g(x)
min即可.
g′(x)=-[1-x+ln(x+1)].
令
ϕ(x)=1-x+ln(x+1)(x>0)⇒ϕ′(x)=-<0∴ϕ(x)在(0,+∞)上单调递减,
又ϕ(2)=ln3-1>0,ϕ(3)=2ln2-2<0,
则存在实数t∈(2,3),使ϕ(t)=0,即t=1+ln(t+1)
∴g(x)在(0,t)上递减,在(t,+∞)上递增.
∴
g(x)min=g(t)==t+1∈(3,4),
故k
max=3.
点评:本题考查利用导函数求函数的单调性、利用函数的单调性求函数的最值、通过构造函数证明不等式的数学思想方法在解题中的应用.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案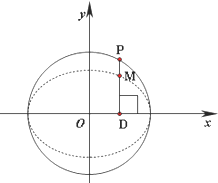 如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且
如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且