
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.

(1)求证:平面EAC⊥平面PBC;
(2)若二面角P-AC-E的余弦值为 ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
(1)见解析(2)
【解析】(1)∵PC⊥平面ABCD,AC?平面ABCD,∴AC⊥PC.∵AB=2,AD=CD=1,∴AC=BC= .
.
∴AC2+BC2=AB2.∴AC⊥BC.
又BC∩PC=C,∴AC⊥平面PBC.
∵AC?平面EAC,
∴平面EAC⊥平面PBC.
(2)如图,以点C为原点, ,
, ,
, 分别为x轴、y轴、z轴正方向,建立空间直角坐标系,
分别为x轴、y轴、z轴正方向,建立空间直角坐标系,

则C(0,0,0),A(1,1,0),B(1,-1,0),设P(0,0,a)(a>0),
则E ,
, =(1,1,0),
=(1,1,0), =(0,0,a),
=(0,0,a), =
= .取m=(1,-1,0),则m·
.取m=(1,-1,0),则m· =m·
=m· =0,m为面PAC的法向量.设n=(x,y,z)为面EAC的法向量,则n·
=0,m为面PAC的法向量.设n=(x,y,z)为面EAC的法向量,则n· =n·
=n· =0,即
=0,即 取x=a,y=-a,z=-2,则n=(a,-a,-2),依题意,|cos〈m,n〉|=
取x=a,y=-a,z=-2,则n=(a,-a,-2),依题意,|cos〈m,n〉|= =
=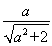 =
= ,则a=2.于是n=(2,-2,-2),
,则a=2.于是n=(2,-2,-2), =(1,1,-2).设直线PA与平面EAC所成角为θ,则sin θ=|cos〈
=(1,1,-2).设直线PA与平面EAC所成角为θ,则sin θ=|cos〈 ,n〉|=
,n〉|= =
= ,即直线PA与平面EAC所成角的正弦值为
,即直线PA与平面EAC所成角的正弦值为


科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用2练习卷(解析版) 题型:填空题
已知[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.2]=-2.x0是函数f(x)=ln x- 的零点,则[x0]=________.
的零点,则[x0]=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用1练习卷(解析版) 题型:填空题
已知函数y=f(x)是R上的偶函数,对?x∈R都有f(x+4)=f(x)+f(2)成立.当x1,x2∈[0,2],且x1≠x2时,都有 <0,给出下列命题:
<0,给出下列命题:
①f(2)=0;
②直线x=-4是函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[-4,4]上有四个零点;
④f(2 014)=0.
其中所有正确命题的序号为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用18练习卷(解析版) 题型:解答题
已知(1+x)n=a0+a1(x-1)+a2(x-1)2+…+an(x-1)n(n∈N*).
(1)求a0及Sn=a1+a2+a3+…+an;
(2)试比较Sn与(n-2)2n+2n2的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用17练习卷(解析版) 题型:解答题
一投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分.经过多次试验,某人投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋.
(1)求该人在4次投掷中恰有三次投入红袋的概率;
(2)求该人两次投掷后得分ξ的数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用15练习卷(解析版) 题型:解答题
已知曲线C1: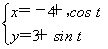 (t为参数),C2:
(t为参数),C2:
(θ为参数).
(1)化C1、C2的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C1上的点P对应的参数为t= ,Q为C2上的动点,求PQ中点M到直线C3:
,Q为C2上的动点,求PQ中点M到直线C3: (t为参数)距离的最小值.
(t为参数)距离的最小值.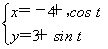
解
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(解析版) 题型:填空题
设椭圆C∶ =1(a>b>0)恒过定点A(1,2),则椭圆的中心到准线的距离的最小值________.
=1(a>b>0)恒过定点A(1,2),则椭圆的中心到准线的距离的最小值________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练4练习卷(解析版) 题型:选择题
执行如图所示的程序框图,若输出的b的值为16,则图中判断框内①处应填( )

A.2 B.3
C.4 D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com