练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    甲乙两个班级均为40人，进行一门考试后，按学生考试成绩及格与不及格进行统计，甲班及格人数为36人，乙班及格人数为24人．
    （1）根据以上数据建立一个的列联表；（2）试判断成绩与班级是否有关？ 
    参考公式：；
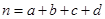
    P(K2>k)
    		0．50
    		0．40
    		0．25
    		0．15
    		0．10
    		0．05
    		0．025
    		0．010
    		0．005
    		0．001
      k
    		0．455
    		0．708
    		1．323
    		2．072
    		2．706
    		3．84
    		5．024
    		6．635
    		7．879
    		10．83
     
    （1）列联表见解析；（2）成绩与班级有关．

    试题分析：（1）由题目中所给数据及列联表概念可列出表格；（2）独立性检验需先求出，用查表比较与临界值的大小，判断出两者在多大上可以认为两者相关．
    解：（1）2×2列联表如下：
     
    		不及格
    		及格
    		总计
    甲班
    		4
    		36
    		40
    乙班
    		16
    		24
    		40
    总计
    		20
    		60
    		80
     
    （2）
    由，所以有99．5%的把握认为“成绩与班级有关系”．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    为调查某市老年人是否需要志愿者提供帮助，用简单随机抽样方法从该市调查了500位老年人，结果如右表.
    性别
    是否需要志愿者
    		男
    		女
    需要
    		40
    		30
    不需要
    		160
    		270
     
    （1）估计该市老年人中， 需要志愿者提供帮助的老年人的比例；
    （2）能否有99%的把握认为该市的老年人是否需要志愿者提供帮助与性别有关？
    附：(）

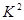
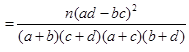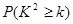    		0.050
    		0.010
    		0.001

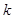    		3.841
    		6.635
    		10.828
     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某地区2007年至2013年农村居民家庭纯收入y（单位：千元）的数据如下表：
    年份
    		2007
    		2008
    		2009
    		2010
    		2011
    		2012
    		2013
    年份代号t
    		1
    		2
    		3
    		4
    		5
    		6
    		7
    人均纯收入y
    		2.9
    		3.3
    		3.6
    		4.4
    		4.8
    		5.2
    		5.9
     
    （1）求y关于t的线性回归方程；
    （2）利用（1）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.
    附：回归直线的斜率和截距的最小二乘法估计公式分别为：
    ，

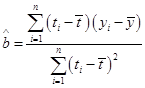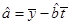
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示：
     
    		积极参加班级工作
    		不太主动参加班级工作
    		合计
    学习积极性高
    		18
    		7
    		25
    学习积极性一般
    		6
    		19
    		25
    合计
    		24
    		26
    		50
     
    (1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少？抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少？
    (2)试运用独立性检验的思想方法点拨：学生的学习积极性与对待班级工作的态度是否有关系？并说明理由．(参考下表)
    P(K2≥k)
    		0．50
    		0．40
    		0．25
    		0．15
    		0．10
    		0．05
    		0．025
    		0．010
    		0．005
    		0．001
    k
    		0．455
    		0．708
    		1．323
    		2．072
    		2．706
    		3．841
    		5．024
    		6．635
    		7．879
    		10．828
     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某校高中生共有2700人，其中高一年级900人，高二年级1200人，高三年级600人，现采取分层抽样法抽取容量为135的样本，那么高一，高二，高三各年级抽取的人数分别为（　　）
    A．45，75，15B．45，45，45C．30，90，15D．45，60，30

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    电视传媒为了解某市100万观众对足球节目的收视情况，随机抽取了100名观众进行调查．如图是根据调查结果绘制的观众每周平均收看足球节目时间的频率分布直方图，将每周平均收看足球节目时间不低于1.5小时的观众称为“足球迷”，并将其中每周平均收看足球节目时间不低于2.5小时的观众称为“铁杆足球迷”．
    （1）试估算该市“足球迷”的人数，并指出其中“铁杆足球迷”约为多少人；
    （2）该市要举办一场足球比赛，已知该市的足球场可容纳10万名观众．根据调查，如果票价定为100元/张，则非“足球迷”均不会到现场观看，而“足球迷”均愿意前往现场观看．如果票价提高元/张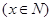，则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少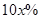，“铁杆足球迷”愿意前往观看的人数会减少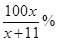．问票价至少定为多少元/张时，才能使前往现场观看足球比赛的人数不超过10万人？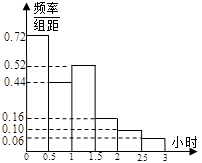

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

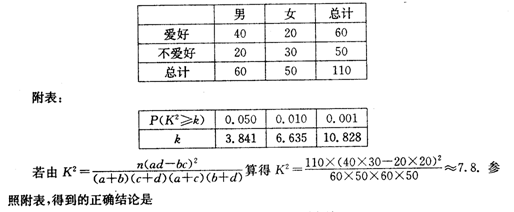
    通过随机调查110名性别不同的学生是否爱好某项运动，得到如下的列联表：
    A．有99％以上的把握认为“爱好该项运动与性别有关”
    B．有99％以上的把握认为“爱好该项运动与性别无关”
    C．在犯错误的概率不超过0．1％的前提下，认为“爱好该项运动与性别有关”
    D．在犯错误的概率不超过0．1％的前提下，认为“爱好该项运动与性别无关”

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验．
    根据收集到的数据（如下表），由最小二乘法求得回归方程
    零件数x(个)
    		10
    		20
    		30
    		40
    		50
    加工时间y（min）
    		62
    		m
    		n
    		81
    		89
     
    则m+n的值为：
    A．137    B．129    C．121     D．118

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

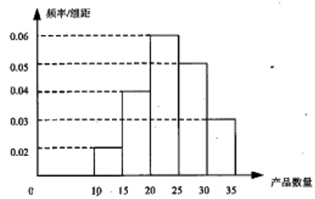
    为了调查某厂2000名工人生产某种产品的能力，随机抽查了位工人某天生产该产品的数量，产品数量的分组区间为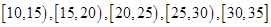，得到如题（16）图所示的频率分布直方图。已知生产的产品数量在之间的工人有6位.
    （1）求；
    （2）工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训，求这2位工人不在同一组的概率.

    查看答案和解析>>

    同步练习册答案