
在直角坐标系xOy中,曲线Cl的参数方程为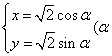 为参
为参
数),以原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为
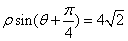
(I)求曲线Cl的普通方程与曲线C2的直角坐标方程;
(Ⅱ)设P为曲线C1上的动点,求点P到C2上点的距离的最小值,并求此时点P的直角坐标.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
定义:若函数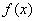 的图象经过变换T后所得图象对应函数
的图象经过变换T后所得图象对应函数
的值域与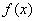 的值域相同,则称变换T是
的值域相同,则称变换T是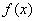 的“同值变换”,
的“同值变换”,
下面给出四个函数及其对应的变换T,其中T不属于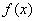
的“同值变换”的是
A.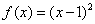 ,T:将函数
,T:将函数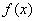 的图象关于y轴对称
的图象关于y轴对称
` B.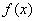 =2x-l-1,T:将函数
=2x-l-1,T:将函数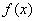 的图象关于x轴对称
的图象关于x轴对称
C.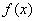 =2x+3,T:将函数
=2x+3,T:将函数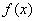 的图象关于点(-1,1)对称’
的图象关于点(-1,1)对称’
D.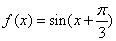 ,T:将函数
,T:将函数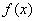 的图象关于点(一1,0)对称
的图象关于点(一1,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
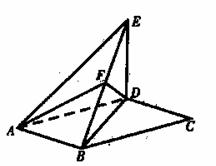
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4;将
△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD。
(1)求证:AB⊥DE;
(2)若点F为BE的中点,求直线AF与平面ADE所成角正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
一艘轮船在航行中燃料费和它的速度的立方成正比, k为比例常数.已知速度为每小时10千米时,燃料费是每小时6元,而其它与速度无关的费用是每小时96元,问轮船的速度是多少时,航行1千米所需的费用总和为最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
两条直线y=x+2a,y=2x+a的交点P在圆(x-1)2+(y-1)2=4的内部,则实数a的取值范围是( ).
A. 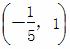 B.
B. 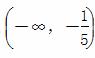 ∪(1,+∞)
∪(1,+∞)
C. 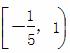 D.
D. 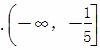 ∪[1,+∞)
∪[1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com