
分析 (1)采用分析法推导使结论成立的条件即可;
(2)根据三角形两边之和大于第三边代入式子即可得出结论.
解答 证明:(1)欲证${({\sqrt{a}-\sqrt{b}})^2}<\frac{{{{({a-b})}^2}}}{4b}$,
只需证$1<\frac{{{{({\sqrt{a}+\sqrt{b}})}^2}}}{4b}$,
即证$1<\frac{{a+b+2\sqrt{a}\sqrt{b}}}{4b}$
∵a>b>0,∴$\frac{a+b+2\sqrt{a}\sqrt{b}}{4b}$>$\frac{b+b+2\sqrt{b}\sqrt{b}}{4b}$=1.
∴(${\sqrt{a}$-$\sqrt{b}}$)2<$\frac{{{{({a-b})}^2}}}{4b}$.
(2)∵a+b>c,b+c>a,a+c>b,
∴a2+b2+c2<a(b+c)+b(a+c)+c(a+b)=2(ab+bc+ca).
∴a2+b2+c2<2(ab+bc+ca).
点评 本题考查了不等式的证明方法,属于中档题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{x^2}+5}}{{\sqrt{{x^2}+4}}}$ | B. | $\frac{b}{a}$+$\frac{a}{b}$ | C. | 2x+$\frac{1}{2^x}$ | D. | cosx+$\frac{1}{cosx}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
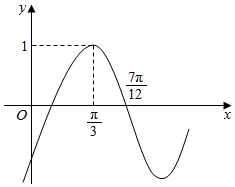 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如下结论中正确的是( )
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如下结论中正确的是( )| A. | f(x)图象C关于直线x=$\frac{11}{12}$π对称 | |
| B. | f(x)图象C关于点($\frac{2π}{3}$,0)对称 | |
| C. | 函数f(x)在区间($\frac{5π}{6}$,$\frac{4π}{3}$)内是增函数 | |
| D. | 把y=sin2x向右平移$\frac{π}{3}$个单位可以得到f(x)的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
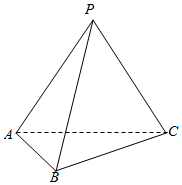 如图,在三棱锥P-ABC中,PA=PC=5,PB=4,AB=BC=2$\sqrt{3}$,∠ACB=30°.
如图,在三棱锥P-ABC中,PA=PC=5,PB=4,AB=BC=2$\sqrt{3}$,∠ACB=30°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 锐角三角形 | C. | 任意三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com