
在 中,角
中,角 所对的边分别是
所对的边分别是 ,已知
,已知 .
.
(Ⅰ)若 的面积等于
的面积等于 ,求
,求 ;
;
(Ⅱ)若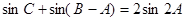 ,求
,求 的面积.
的面积.
(Ⅰ)2,2(Ⅱ)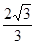
解析试题分析:(Ⅰ)由 ,运用余弦定理可得
,运用余弦定理可得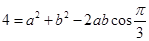 ,由
,由 的面积等于
的面积等于 ,运用三角形面积公式可得,
,运用三角形面积公式可得,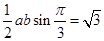 ,联立即可解得
,联立即可解得 ;(Ⅱ)利用三角形内角和定理先将
;(Ⅱ)利用三角形内角和定理先将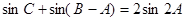 化为
化为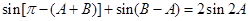 ,利用诱导公式及两角和与差的正弦公式将上式化为
,利用诱导公式及两角和与差的正弦公式将上式化为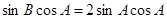 ,分两种情况,若
,分两种情况,若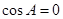 ,则求出A,B,C三角,利用解直角三角形求出
,则求出A,B,C三角,利用解直角三角形求出 ,从而求出面积,若
,从而求出面积,若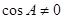 ,求出A,B关系,利用正弦定理求出
,求出A,B关系,利用正弦定理求出 关系,结合(Ⅰ)中结果
关系,结合(Ⅰ)中结果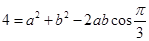 求出
求出 ,从而求出三角形面积.
,从而求出三角形面积.
试题解析:(Ⅰ)由余弦定理及已知条件得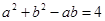
又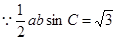 ,得
,得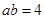 3分
3分
联立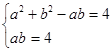 解得
解得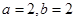 5分
5分
(Ⅱ)由题意得,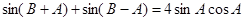
即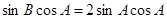 . 7分
. 7分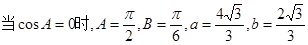
 的面积
的面积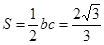 9分
9分
当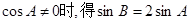 ,由正弦定理得
,由正弦定理得 ,
,
联立方程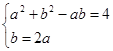
解得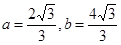
所以 的面积
的面积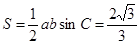 ,综上,
,综上, 的面积为
的面积为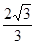 . 12分
. 12分
考点:正弦定理,余弦定理,三角形面积公式,三角变换,运算求解能力


科目:高中数学 来源: 题型:解答题
地面上有两座塔AB、CD,相距120米,一人分别在两塔底部测得一塔顶仰角为另一塔顶仰角的2倍,在两塔底连线的中点O测得两塔顶的仰角互为余角,求两座塔的高度。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com